easy for 1 graders
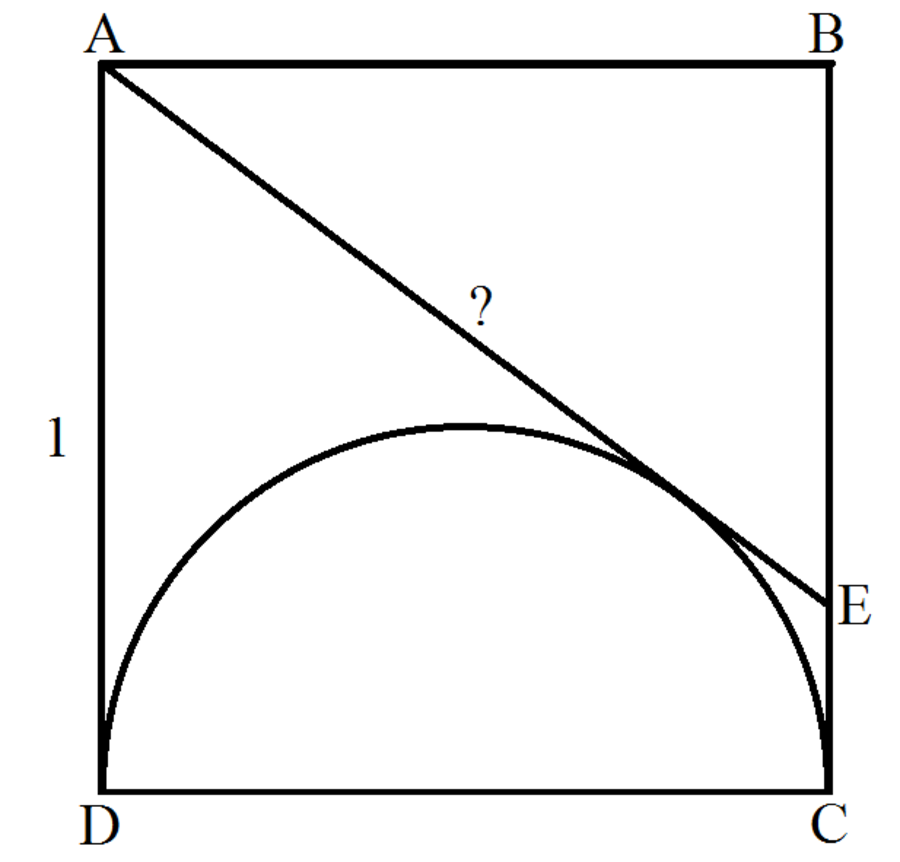
In the figure above, A B C D is a unit square with D C being the diameter of a semicircle. Point E is on B C and line A E is tangent to the semicircle.
Find the length of A E .
The answer is 1.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let us choose the origin of coordinates to be the bottom left corner of the square, lower horizontal side as the X -axis and the left vertical side as the Y -axis. The top left corner of the square, say A , has coordinates ( 0 , 1 ) . Let the tangent to the semicircle through A makes an angle ( π − α ) with the positive X -axis. Then it's equation is y = 1 − x tan α . The equation of the semicircle is x 2 − x + y 2 = 0 . Since the line y = 1 − x tan α touches it, we have ( 1 + 2 tan α ) 2 = 4 × 1 × ( 1 + tan 2 α ) . This yields tan α = 4 3 , and the required length of the line segment is 1 × sec α = 4 5 = 1 . 2 5 . (Since the length of side of square is 1 ).
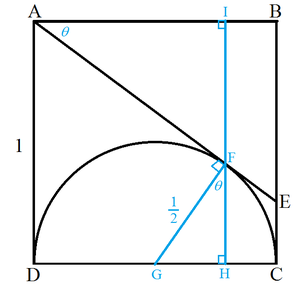
Let the point A E tangent to the semicircle be F and the center of the semicircle be G . Line I H through F is parallel to B C . Then △ F G H and △ A F I are similar with ∠ G F H = ∠ F A I = θ . Then
I F + F H A I tan θ + G F cos θ D H tan θ + 2 1 cos θ ( D G + G H ) tan θ + 2 1 cos θ ( 2 1 + G F sin θ ) tan θ + 2 1 cos θ ( 2 1 + 2 1 sin θ ) tan θ + 2 1 cos θ sin θ + sin 2 θ + cos 2 θ 2 cos θ − sin θ 5 sin ( tan − 1 2 − θ ) tan ( tan − 1 2 − θ ) 1 + 2 tan θ 2 − tan θ 4 − 2 tan θ ⟹ tan θ = 1 = 1 = 1 = 1 = 1 = 1 = 2 cos θ = 1 = 1 = 2 1 = 2 1 = 1 + 2 tan θ = 4 3 Multiply both sides by 2 cos θ ⟹ sin ( tan − 1 2 − θ ) = 5 1
Therefore A E = cos θ A B = 4 5 = 1 . 2 5 .
@Chew-Seong Cheong What did you do to go from "sin(θ) + sin^2(θ) + cos^2(θ) = 2cos(θ)" to "2cos(θ) - sin(θ) = 1"?
Log in to reply
sin 2 θ + cos 2 θ = 1 . You can enter in LaTex as \ ( \sin \theta + \sin^2 \theta + \cos^2 \theta = 2 \cos \theta \ )
@Mariothedog . s i n 2 ( θ ) + c o s 2 ( θ ) = 1 is the pythagoras identity.
Let P be the point of tangency, and let O be the midpoint of D C . Then triangles A P O and A D O are both right triangles with the same hypotenuse and same short leg length 0 . 5 , so they are congruent. Hence A P = 1 . In the same way, we can see that O P E and O C E are congruent right triangles. Now there are a couple of ways to proceed:
(1) Let P E = E C = a . Then A E = 1 + a , and A B = 1 and B E = 1 − a , so Pythagoras gives ( 1 − a ) 2 + 1 2 − 2 a + 1 = ( 1 + a ) 2 = 2 a so a = 1 / 4 and hence A E = 5 / 4 = 1 . 2 5 .
(2) ∠ A O D = ∠ A O P , and ∠ P O E = ∠ C O E , but all four of these angles add up to 1 8 0 o , so ∠ A O P + ∠ P O E = 9 0 o , so triangle A O E is a right triangle. Then it's easy to see that all of the triangles we have considered ( A D O , A P O , O P E , O C E , A O E ) are similar right triangles, where the long leg is twice the short leg. So the short leg P E of O P E is half the long leg O P , which is 1 / 2 , so P E = 1 / 4 and A E = 5 / 4 = 1 . 2 5 .
Link to my solution on YouTube .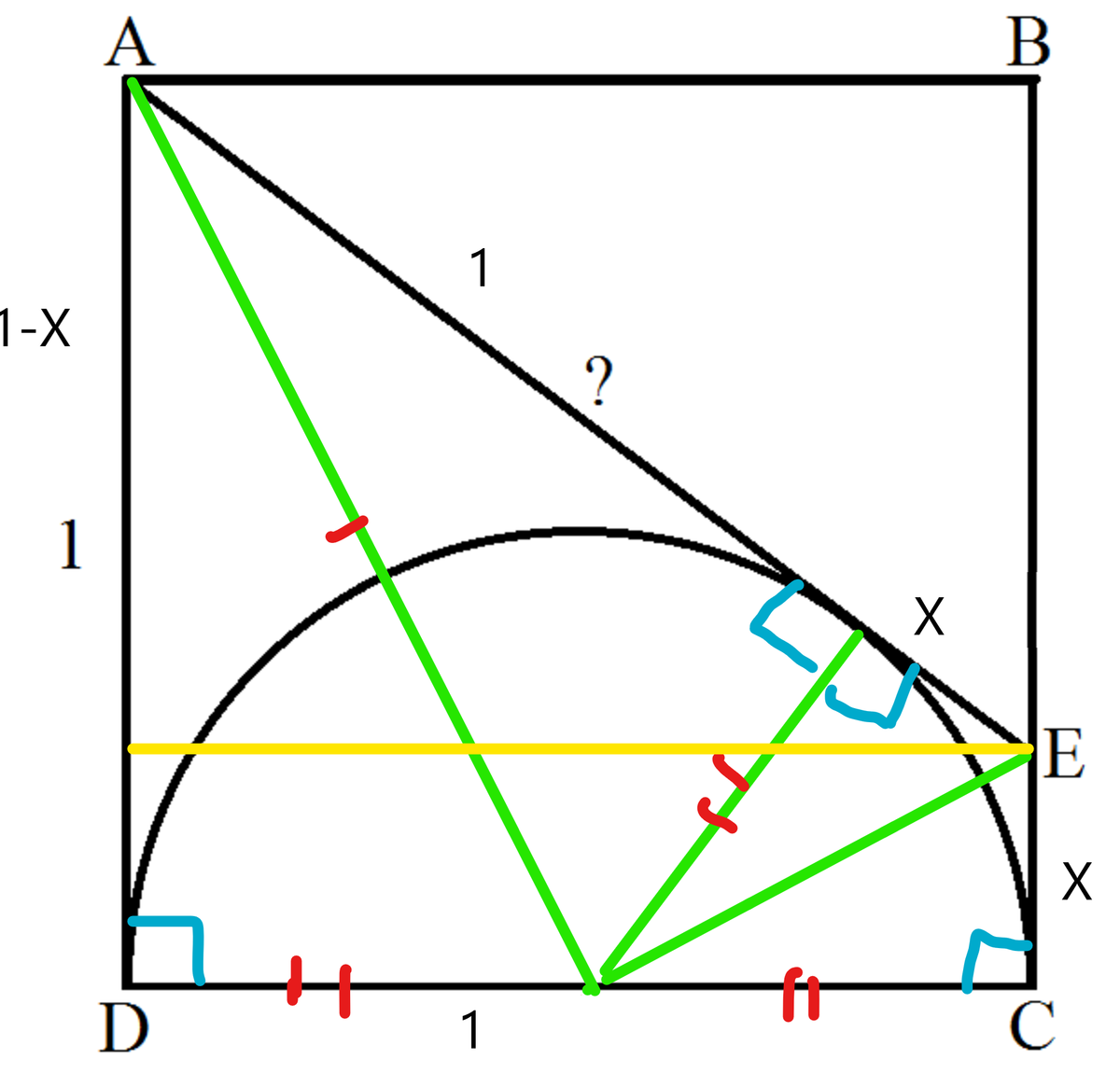 As shown in the diagram above, we can add lines to construct two pairs of congruent triangles. They are congruent because of the RHS congruence rule.
Then we can use the Pythagoras theorem to show that
(
1
−
x
)
2
+
1
2
=
(
1
+
x
)
2
and we get
x
=
0
.
2
5
Since AE is
1
+
x
, therefore the answer is
1
.
2
5
.
As shown in the diagram above, we can add lines to construct two pairs of congruent triangles. They are congruent because of the RHS congruence rule.
Then we can use the Pythagoras theorem to show that
(
1
−
x
)
2
+
1
2
=
(
1
+
x
)
2
and we get
x
=
0
.
2
5
Since AE is
1
+
x
, therefore the answer is
1
.
2
5
.