Easy geometry!
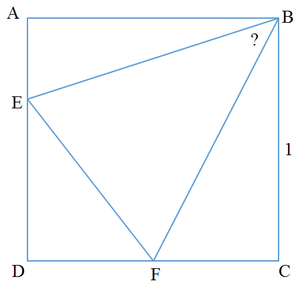
A B C D is a square with side length of 1. △ B E F inscribed in the square is such that E is on A D and F is on C D . Perimeter of △ D E F is 2. Find the measure of ∠ E B F .
Bonus : Use geometry only.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
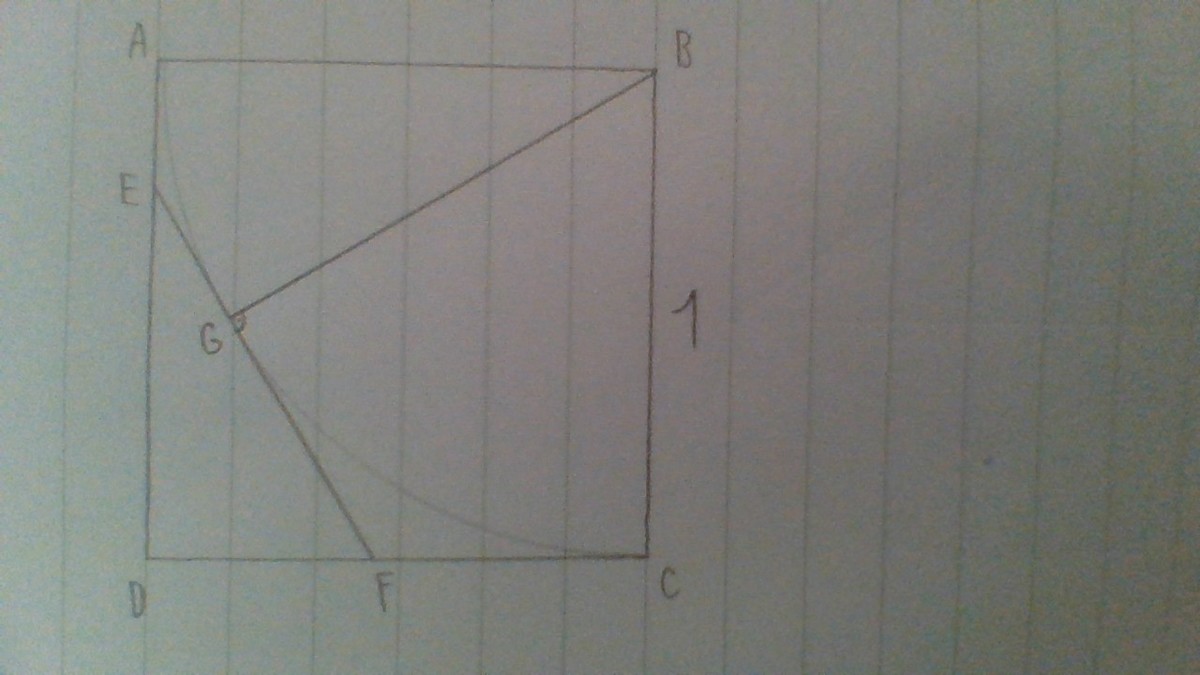 If we draw a circle with center at B and radius equal to |AB| = 1, we know that the perimeter of any triangle DEF, which has got EF tangent to the circle is equal to 2, because |AE|=|EG| and |FG|=|FC| so the perimeter of triangle DEF is equal to |AD| + |CD| = 2. Now to prove that these triangles DEF are the only ones with perimeter 2 we can consider this: Draw any other line segment E´F´ and we can for every E´F´ find paralel line which is tangent to the quarter circle. Because
If we draw a circle with center at B and radius equal to |AB| = 1, we know that the perimeter of any triangle DEF, which has got EF tangent to the circle is equal to 2, because |AE|=|EG| and |FG|=|FC| so the perimeter of triangle DEF is equal to |AD| + |CD| = 2. Now to prove that these triangles DEF are the only ones with perimeter 2 we can consider this: Draw any other line segment E´F´ and we can for every E´F´ find paralel line which is tangent to the quarter circle. Because
E´F´ and the new tangent lines are paralel we can say that triangles DE´F´ and a new triangle made by the paralel line are similar with coeficient of similarity not equal to 1 (because line E´F´ is not same as the new line) so the perimeter is not equal to 2. Now we can easly calculate angle EBF as a half of the sum of angles ABG and GBC so it is 45°.
Let D F = x and D E = y . Since the perimeter of △ D E F is 2,
x + y + x 2 + y 2 x + y − 2 x 2 + 2 x y + y 2 − 4 ( x + y ) + 4 ⟹ x y = 2 = x 2 + y 2 = x 2 + y 2 = 2 ( x + y − 1 ) Squaring both sides
Let ∠ E B F = θ . Then
θ = 9 0 ∘ − tan − 1 ( 1 − x ) − tan − 1 ( 1 − y ) = 9 0 ∘ − tan − 1 ( 1 − ( 1 − x ) ( 1 − y ) 1 − x + 1 − y ) = 9 0 ∘ − tan − 1 ( x + y − x y 2 − x − y ) = 9 0 ∘ − tan − 1 ( x + y − x y 2 − x − y ) = 9 0 ∘ − tan − 1 ( 2 − x − y 2 − x − y ) = 9 0 ∘ − tan − 1 ( 1 ) = 9 0 ∘ − 4 5 ∘ = = 4 5 ∘ Note that x y = 2 ( x + y − 1 )
Please ask if you don't understand my writing