Circles in a Square

Let the square be $ABCD$ and the centers of the big and small circles be $O$ and $P$ respectively.

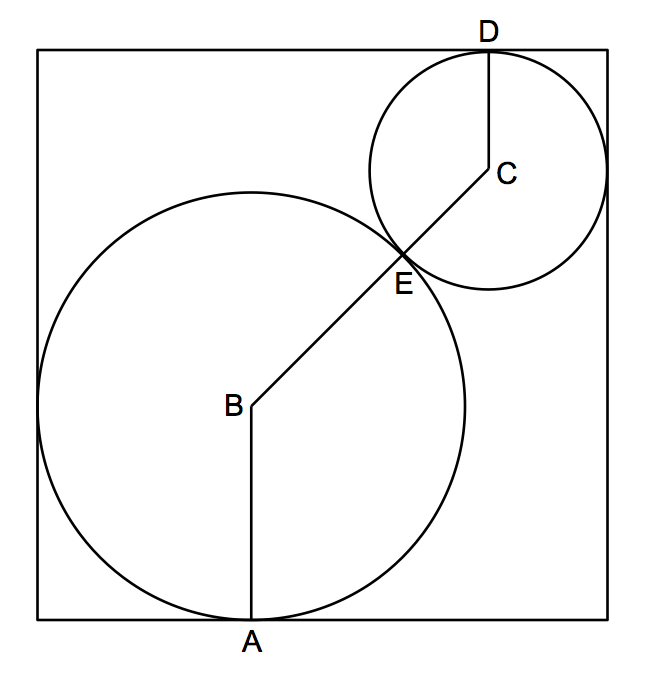We note that $\space BP = r\sqrt{2}$ , $\space OD = R\sqrt{2} \space$ and

$\quad BD = BP+PO+OD = r\sqrt{2} + r + R + R\sqrt{2} = (R+r)(1+\sqrt{2})$

We note also that $BD = (2+\sqrt{2}) \times \sqrt{2} = 2\sqrt{2}+2 = 2(1+\sqrt{2})$

Therefore, $\quad (R+r)(1+\sqrt{2}) = 2(1+\sqrt{2})\quad \Rightarrow R+r = \boxed{2}$

Note that $AB=BE= R$ and that $EC=CD= r$ . Then $BC= R + r$ and $BC$ is along the diagonal of the square. This means that $BC$ is the hypotenuse of a 45-45-90 triangle. Let the length of the leg of this triangle be $x$ . We proceed as follows:

Side length of square $=2+\sqrt{2}=AB+ x +CD$

$2+\sqrt{2}= R + r + x$

$x \sqrt{2}=BC= R + r$

$x =\dfrac{ R + r }{\sqrt{2}}$

$2+\sqrt{2}= R + r +\dfrac{ R + r }{\sqrt{2}}$

$2+\sqrt{2}=( R + r )(1+\dfrac{1}{\sqrt{2}})$

$2= R + r$

Anti-solution: Because the problem does not give any information of exactly what $R$ and $r$ are, the answer must be independent of $R$ and $r$ (i.e: $R+r$ is an invariant). This must continue to hold even if $r$ is zero (assuming we "accidentally" glanced over the "inside the square" part). At this point, the large circle with radius $R$ is tangent to two sides of the square and intersects a corner. It is easily shown that in this case, $R=2$ . $R+r = 2+0 = 2$ .

My actual solution: The distance between the center of the large circle and the corner of the square is $R\sqrt{2}$ . Likewise, the distance between the center of the small circle and its corner of the square is $r\sqrt{2}$ . The distance between the centers of the circles is $R+r$ . So, the total distance is $(R+r)(1+\sqrt{2})$ . This must be equal to the diagonal of the square, $2\sqrt{2}+2$ . Solving $(R+r)(1+\sqrt{2})=2\sqrt{2}+2$ Results in the answer of $R+r=2$ .

Edit: Realized my solution is effectively the same as Chew-Seong Cheong's but I'll keep it anyway.

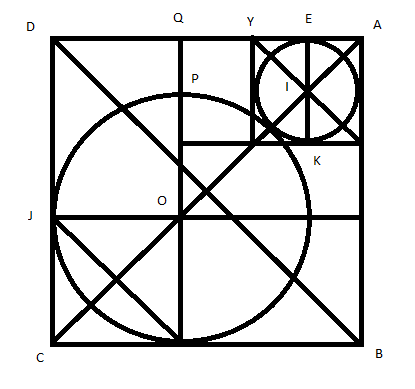$EA+CJ=EA+DQ=DA-QE=OA-IA$ $=\sqrt{2}AB-\sqrt{2}DQ-\sqrt{2}EA$ $\sqrt{2}AB-\sqrt{2}DQ-\sqrt{2}EA=DQ+EA$ $(DQ+EA)(1+\sqrt{2})=\sqrt{2}AB$ $(DQ+EA)=\frac{(\sqrt{2}AB)}{(1+\sqrt{2})}$ $DQ+EA=\frac{(\sqrt{2}AB)}{(1+\sqrt{2})}$ $DQ+EA=\frac{(\sqrt{2}(2+\sqrt{2}))}{(1+\sqrt{2})}$ $DQ+EA=\frac{(\sqrt{2} \times \sqrt{2} \times (1+\sqrt{2}))}{(1+\sqrt{2})}=\boxed{2}$