A geometry problem by Lee Dongheng
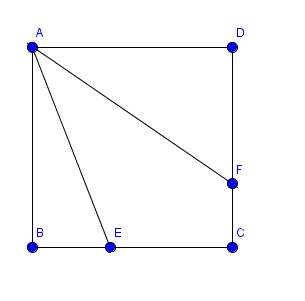 The figure shows a square
A
B
C
D
.
E
and
F
are selected on
B
C
and
C
D
respectively such that
∠
D
A
F
=
∠
E
A
F
,
A
E
=
2
0
2
,
B
E
=
1
1
6
, find the length of
D
F
.
The figure shows a square
A
B
C
D
.
E
and
F
are selected on
B
C
and
C
D
respectively such that
∠
D
A
F
=
∠
E
A
F
,
A
E
=
2
0
2
,
B
E
=
1
1
6
, find the length of
D
F
.
Note : The figure is not drawn to scale.
The answer is 86.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I have proven that AE = BE + DF :) It's Included in my solution. Sorry if it's too long or convoluted. It's the only way I can see it. hahahaha
A D = A B = A E 2 + B E 2 = 2 0 2 2 + 1 1 6 2 = 2 7 3 4 8 = 2 6 8 3 7
∠ B A E = 9 0 − 2 ∠ D A F
∠ A E B = 9 0 − ∠ B A E = 9 0 − ( 9 0 − 2 ∠ D A F ) = 2 ∠ D A F
cos ∠ A E B = cos 2 ∠ D A F = 2 0 2 1 1 6 = 1 0 1 5 8
2 ∠ D A F = arccos ( 1 0 1 5 8 )
∠ D A F = 2 1 arccos ( 1 0 1 5 8 )
tan ∠ D A F = 2 6 8 3 7 D F
D F = 2 6 8 3 7 tan ∠ D A F
D F = 2 6 8 3 7 tan ( 2 1 arccos ( 1 0 1 5 8 ) ) = 8 6
And;
To prove that A E = B E + D F
cos ( 2 ∠ D A F ) = A E B E ⇒ B E = A E cos ( 2 ∠ D A F ) ⇒ B E = A E ( cos 2 ∠ D A F − sin 2 ∠ D A F )
sin ( 2 ∠ D A F ) = A E A B ⇒ A B = A E sin ( 2 ∠ D A F ) ⇒ A B = 2 ( A E ) ( cos ∠ D A F ) ( sin ∠ D A F )
t a n ∠ D A F = A D D F = A B D F ⇒ A B = tan ∠ D A F D F ⇒ A B = sin ∠ D A F D F cos ∠ D A F
2 ( A E ) ( cos ∠ D A F ) ( sin ∠ D A F ) = sin ∠ D A F D F cos ∠ D A F
D F = 2 ( A E ) ( s i n 2 ∠ D A F )
B E + D F = A E ( cos 2 ∠ D A F − sin 2 ∠ D A F ) + 2 ( A E ) ( sin 2 ∠ D A F )
B E + D F = A E ( ( cos 2 ∠ D A F − sin 2 ∠ D A F ) + 2 ( sin 2 ∠ D A F ) )
B E + D F = A E ( cos 2 ∠ D A F + sin 2 ∠ D A F )
B E + D F = A E ( 1 )
B E + D F = A E
E C = A B − 1 1 6 , C G = A E − E C = 2 0 2 + 1 1 6 − A B
△ A D F ∼ △ G C F ,
Therefore C F D F = C G A D
A B − x x = 3 1 8 − A B A B
3 1 8 x − A B x = A B 2 − A B x
3 1 8 x = 2 0 2 2 − 1 1 6 2 = ( 2 0 2 + 1 1 6 ) ( 2 0 2 − 1 1 6 )
x = 8 6
Bonus question : Can you prove A E = B E + D F ?