A geometry problem by Ricky Huang
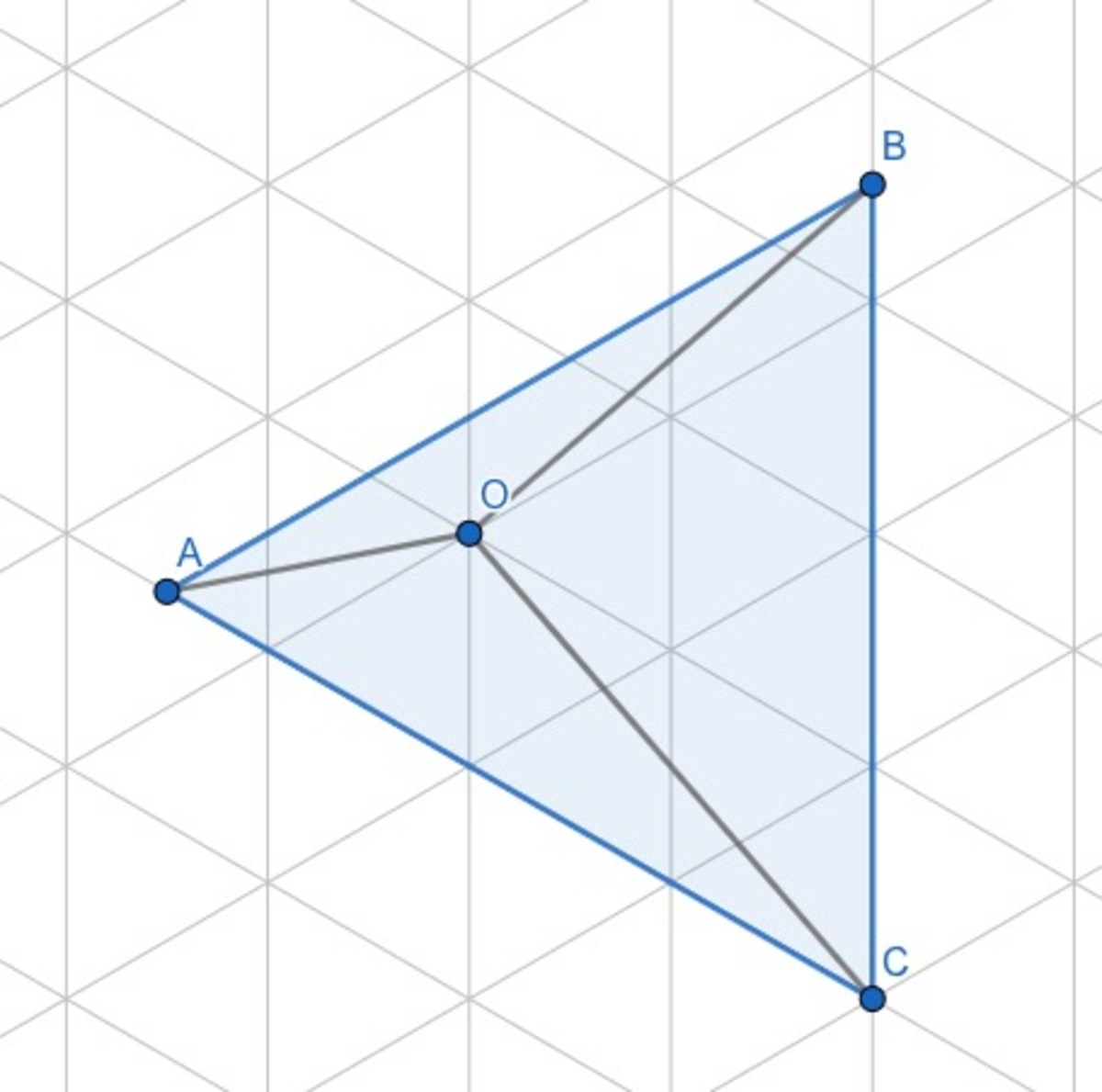 We have an equilateral
and a random point
in it such that
and
. Using lines
,
, and
to make an triangle, which of the answer options cannot be an internal angle of the triangle?
We have an equilateral
and a random point
in it such that
and
. Using lines
,
, and
to make an triangle, which of the answer options cannot be an internal angle of the triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Cut out equilateral triangles △ O P P ′ , △ O Q Q ′ , and △ O R R ′ , as shown below, and rearrange the remaining triangles as follows, so that △ T U V is the new triangle made from A O , B O , and C O :
Then
∠ T = C ′ O ′ A ′ = ∠ A O C − 6 0 ° = x − 6 0 °
∠ U = C ′ O ′ B ′ = ∠ B O C − 6 0 ° = y − 6 0 °
∠ V = 1 8 0 ° − ∠ T − ∠ U = 1 8 0 ° − ( x − 6 0 ° ) − ( y − 6 0 ° ) = 3 0 0 ° − y − x .
Therefore, the internal angle cannot be y − 5 0 ° .