Easy Limits....
Calculus
Level
2
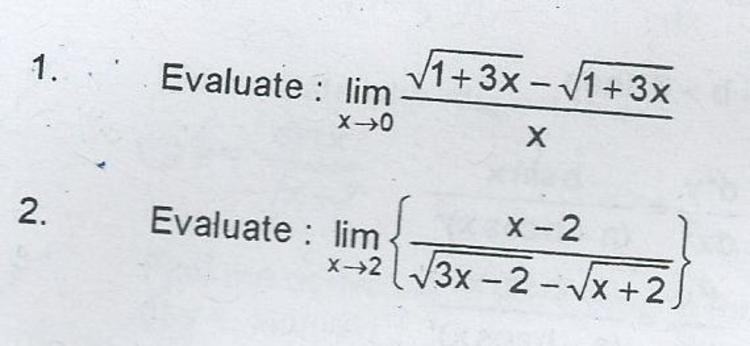The solutions of 1 and 2 are
respectively which are positive integers
Find
36
64
216
1
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we look carefully at the problem, In 1, we would observe that for any value of x other than 0 , we have expression equal to 0.so as x approaches 0 , the expression must be very close to 0.Now , we have been asked b to the power a and a being 0 makes the expression =1, and we need not even evaluate b.