This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Out of curiosity, what would be the fastest way to find the required factors to factorise X 2 − X − 1 9 8 0 = 0 ? I listed all the possible factors, and the 1 7 th pair of factors came to be the required ones. I spent about five minutes listing all the factors.
Log in to reply
@Omkar Kulkarni , it's a quadratic equation. Just use the quadratic formula and you'll get that the roots are x = 4 5 , ( − 4 4 ) .
x = 2 1 ± 1 + 7 9 2 0 = 2 1 ± 8 9 = 4 5 , ( − 4 4 )
That's the fastest one can go with a calculator. There's also the method of middle term factorization that can be used.
Use the formula: 1 3 + 2 3 + 3 3 + . . . . . + n 3 = ( 2 n ( n + 1 ) ) 2 and + 2 + 3 + . . . . . + n = 2 n ( n + 1 )
As the problem follows: ( 2 n ( n + 1 ) ) 2 − 2 n ( n + 1 ) = 1 9 8 0
Combining the fraction and simplifying: n 4 + 2 n 3 − n 2 − n − 7 9 2 0 = 0
Graph it and the approximate positive root is 9 . 9 9 7 which is rounded to 1 0
anshuman shreshth, the conclusion which you reached in the class is already a formulae.
that is the sum of cube of terms of an a.p. is equal to square of the sum of the terms of the a.p. .
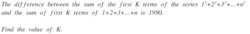
What is given to us is:
i = 1 ∑ K i 3 − i = 1 ∑ K i = 1 9 8 0
We will use two identities: i = 1 ∑ n i 3 = ( 2 n ( n + 1 ) ) 2 and i = 1 ∑ n i = 2 n ( n + 1 )
Let X = 2 K ( K + 1 ) . The given sum can now be written as:
X 2 − X − 1 9 8 0 = 0 ⟹ ( X − 4 5 ) ( X + 4 4 ) = 1 9 8 0 ⟹ X = 4 5
The negative solution is rejected since K cannot be negative and hence X also cannot be negative. Similarly, we'll reject the negative K in the next step. Now,
X = 2 K ( K + 1 ) = 4 5 ⟹ K 2 + K − 9 0 = 0 ⟹ ( K − 9 ) ( K + 1 0 ) = 0 ⟹ K = 9