High On Potenuse
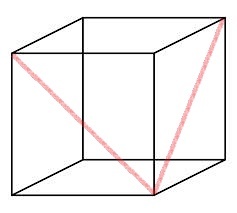 What is the angle made by the two red lines in the cube (answer in degrees)?
What is the angle made by the two red lines in the cube (answer in degrees)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Since he didn't mention the reason for the triangle being equilateral, I'm doing the deed.
Note that each of the sides of the equilateral triangle are actually the diagonals of the front, right and top faces of the cube. And since it's a cube (of say edge length a ), all the sides of the triangle are 2 a using the Pythagorean Theorem:
Diagonal length = a 2 + a 2 = 2 a
Since all the sides of the triangle are equal, it follows from it that the triangle is equilateral and as such, all of its internal angles are equal and sum upto 1 8 0 ∘ . Let the required angle be A . It is trivial now that,
3 A = 1 8 0 ∘ ⟹ A = 6 0 ∘ ⟹ sin ( A ) = 2 3 ⟹ A = arcsin ( 2 3 )
Note: arcsin x and sin − 1 x denote the same thing.
I agree that yours is a shorter solution , but to make your solution more complete you must specify why it is an equilateral triangle .
I know it's easy but I feel that you must add it it :)
Each side of the triangle is a diagonal of identical sized squares, so they are all the same length, so it must be an equalatrial triangle, so each angle is 60 degrees.
But, despite asking for the answer in degrees, the answers are not in degrees. If you don't happen to know what sin 60 is, you might have to use a calculator at this point...
I thought that a solution based on vectors should be there , so here I am !
Assume the length of each edge be a units .

The position vectors of the points A,B and C are given in the pic . Let the origin be O .
A B = B − A = ( − a , a , 0 )
A C = C − A = ( 0 , a , − 1 )
Now lets take the dot product of A B and A C since we are interested in knowing the angle between them .Let the angle be θ
A B ⋅ A C = ∣ A B ∣ ∣ A C ∣ cos θ ⇒ cos θ = a 2 + a 2 + 0 0 + a 2 + a 2 0 + a 2 + 0 = 2 1
Hence the answer is arccos 2 1 = arcsin 2 3
shouldnt it be |AB| |AC| cos(tetha)?
Log in to reply
Yes it should be ! Thanks for the catch :)
If you complete the triangle by adding the 3rd red line, each of the sides is a hypotenuse of a face of the cube. So it's an equilateral triangle, meaning each angle is 6 0 o . Since sin 6 0 = 2 3 , the answer is C.
No need to explain an equilateral triangle in such detail. The diagonals of a cube are all the same length so the triangle edges are all the same length. Therefore it has to be an equilateral triangle
None of the above, since none allow for the specified answer in degrees
The two red lines are two sides of an equilateral triangle
So the measure of the required angle is 60
Draw one more diagonal on the top face connecting the existing red ones. Now it will create an equilateral triangle so angle is 60° i.e. first option.
Each side length of the triangle is sqrt(2) so it is equilateral and each angle is 60 degrees. Simplicity is key.
equilateral triangle, therefore 60 deg
If you join the 3 diagonals of any 3 mutually adjacent faces of a cube, the diagonals form an equilateral triangle.
If I join the end points of those two lines, it will become an equilateral triangle as even after joining endpoints length will remain same as those of other two lines !!
Simply the angle is 60 degree
As the question just state it's a cube, so the sides must be equal ( based on the property of diagonals in a square).
If the cube side length is "a", then length of each red line is \sqrt{a} . similarly the distance bet two ends of the red lines is also \sqrt{a} . Thus it forms an equilateral triangle. And thus angle bet two red lines is 60degree.
The angle is 60° because it is an equilateral triangle which is same as sin^-1(sqrt3/2)