A calculus problem by Parth Lohomi
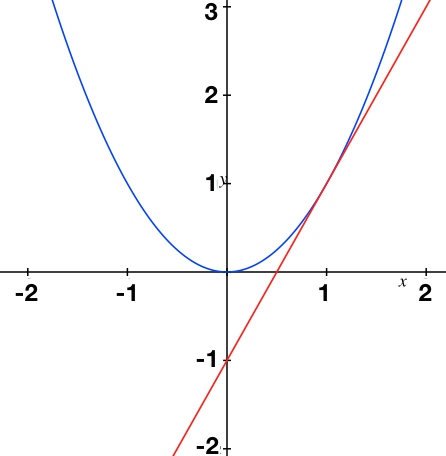
What is the slope of the line tangent to the parabola shown in the figure above?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
this is wrong answer y=x^2 and y'=2x y=mx+c through pass point (0,1) c=-1 and now touching point line and curve we have this equation x^2=2x*x-1then x=+ 1 and -1 and slope of tangent +2 or -2
Log in to reply
The tangent shown in the figure has a slope of 2.
It is clear that the line can't have a negative slope Mohammed
Log in to reply
IN this case(figure) yes but negative answer is acceptable .
It is clear that the line can't have a negative slope @Mohammed Rahimzadeh
Wrong answer n wrong assumption s
Log in to reply
Too many assumptions in this problem. The curve could be y=x^2 and the line does not necessarily cross at (0,-1). Since when do math problems rely on what is seen in a picture?
actually you shouldn't take 0, and ½ though it's right, because that's not made clear. in fact solution to go thus : [1 - (-1)] ÷ [0 - (- 1)]
We can see that the blue graph represents f ( x ) = x 2 . The slope of the tangent line is f ′ ( x 0 ) where x 0 is the point where the line is tangent. We can see that x 0 = 1 so f ′ ( x ) = 2 ∗ x = > f ′ ( 1 ) = 2 so the correct answer is 2.
we can use the equation y=mx+c to find the slope here the red line cuts y- axis at (0,-1) therefore,c = -1 & the line touches the point (1,1) so x=1 & y=1 y=mx+c (1)=m(1)+(-1) 1=m -1 hence, m=2
Mx+4%1=4.3424454545
We have: { y = m x − 1 y = x 2 so m x − 1 = x 2 x 2 − m x + 1 = 0 Here x has only one solution so Δ = 0 b 2 − 4 a c = 0 m 2 − 4 = 0 m 2 = 4 m must be greater than 0 so m = 2 .
We note that the line (red) tangent to the parabola cuts the x -axis and y -axis at ( x 1 , y 1 ) = ( 2 1 , 0 ) and ( x 2 , y 2 ) = ( 0 , − 1 ) respectively. The gradient m of the line is given by:
m = x 2 − x 1 y 2 − y 1 = 0 − 2 1 − 1 − 0 = 2
It can be seen that the parabola is y = x 2 . Therefore its gradient at x is given by d x d y = 2 x . Since the tangent touches the parabola at x = 1 , therefore the gradient is 2 .