What A Mess
{ x + y + z = 2 6 x 1 + y 1 + z 1 = 3 1
The two equations above satisfy the real numbers x , y , z . What is the value of the expression below?
y x + z y + x z + z x + y z + x y
The answer is 803.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
wow! I did the same.
I too did in the same way
Sometimes a simple idea could solve problems that look difficult:)
For example this as easy as
Really simple!
what if we have to find the value of (x+y)xy + (y+z)yz + (x+z)xz @paolaRamieze
x + y = 2 6 − z
x + z = 2 6 − y
z + y = 2 6 − x
You'll get into the same answer...
i am unable to get its answer. please pst how
I did it ur way as well, u just need to break it up into three terms and simplify. U have to do this with the denominator.
Interesting, I'll solve it
y/x + z/x + x/y + z/y + x/z + y/z ( y + z ) / x + ( x + z ) / y + ( x + y ) / z ( 26 - x ) / x + ( 26 - y ) / y + ( 26 - z ) / z 26/x - x/x + 26/y - y / y + 26 /z - z/z 26/x + 26/y + 26/z - 1 -1 -1 26( 1/x + 1/y + 1/z ) - 3 26 x 31 - 3 806 - 3 803
x+y+z=26
1/x + 1/y+ 1/z = 31
x/y+x/z + y/z+y/x + z/x+z/y = k
x( 1/y + 1/z) + y(1/x + 1/z) +z(1/x + 1/y) =k
1/y+ 1/z = 31-1/x 1/x+ 1/z = 31-1/y 1/y+ 1/z = 31-1/z
x( 31-1/x) + y(31-1/y) +z(31-1/z) =k 31x + 31y + 31z -3=k 31(x+y +z) -3=k 31(26) -3=k 803=k
OR
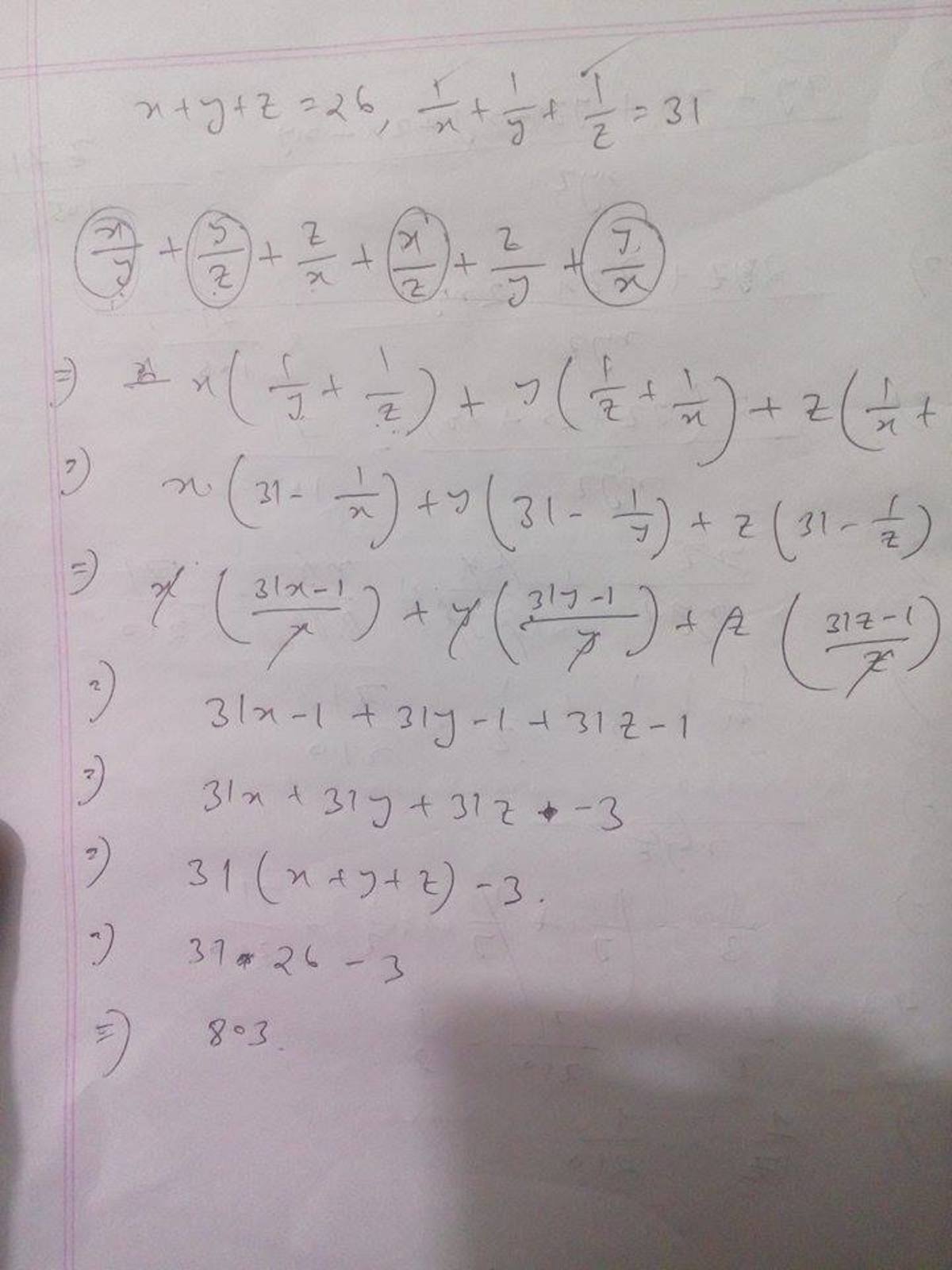
( x + y + z ) ( x 1 + y 1 + z 1 ) = 2 6 × 3 1
y x + z y + x z + z x + y z + x y + 3 = 8 0 6
y x + z y + x z + z x + y z + x y = 8 0 3