Does this relate to Heron?
a + b + c + d a + b + c − d a + b − c + d a − b + c + d − a + b + c + d = = = = = 1 2 1 0 − 2 6 1 0
a , b , c , d are positive integers satisfying the equation above.
What is the value of a × b × c × d ?
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
Great. Can a cyclic quadrilateral with sides a , b , c , d exist?
Nope because since one of the sides (say d) is length 7 then by something similar to the triangle inequality, a + b + c > d because otherwise the lines won't reach the end of the d. However this implies 3 + 1 + 1 > 7 or 5 > 7 which is obviously false.
GREAT Chew-Seong Cheong
a+b+c+d = 12
a+b+c-d = a+b+c+d-2d = 12-2d = 10 -> d=1
a+b-c+d = a+b+c+d-2c = 12-2c = -2 -> c=7
a-b+c+d = a+b+c+d-2b = 12-2b = 6 -> b=3
-a+b+c+d = a+b+c+d-2a = 12-2a = 10 -> a=1
abcd = 1.3.7.1 = 21
Moderator note:
Much simpler! Can you find a way to solve this (as simple as possible) if the first equation is not given?
To the Challenge Master: Just add up the last four given equations (and divide by two) to get the first equation. Then proceed using Robert's method.
Log in to reply
Or, call the first given equation X and the last four A, B, C, and D respectively. You don't want me to use X. Well, how about this: What's A+B+C-D (abusing notation)? A+B-C+D? A-B+C+D? -A+B+C+D?
(Whoah. Those look suspiciously similar to equations A, B, C, and D themselves. Is this a coincidence, or is there something deeper here?)
turning into augmanted matrix:
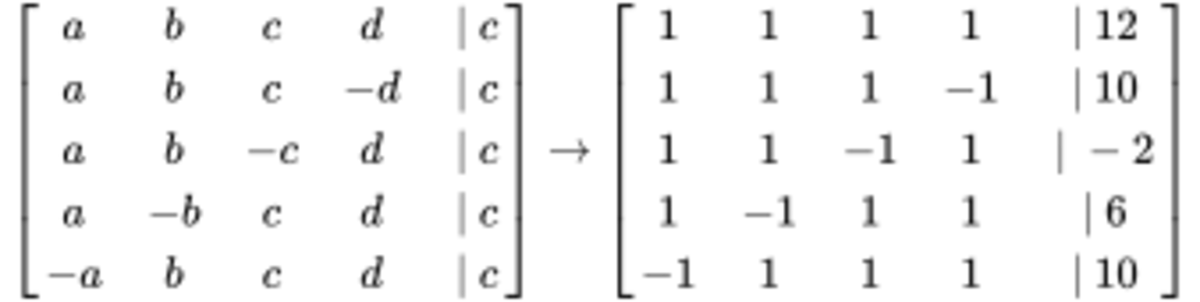
Then subtract row 1 coefficients from all other rows and divide by -2:
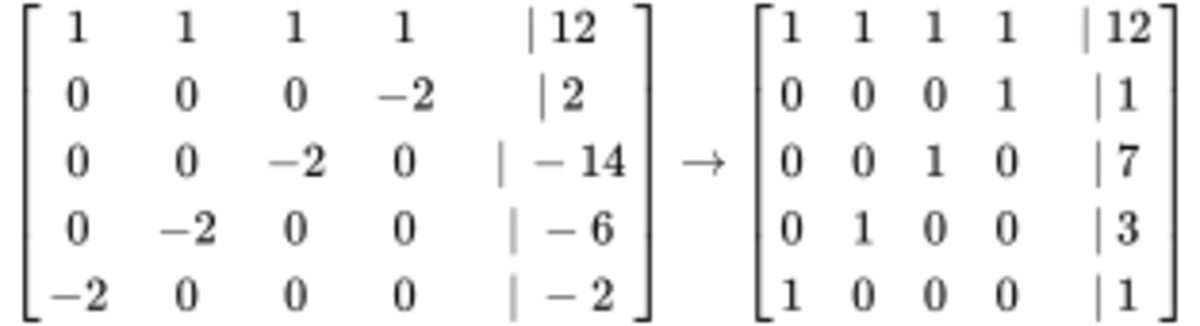
result:
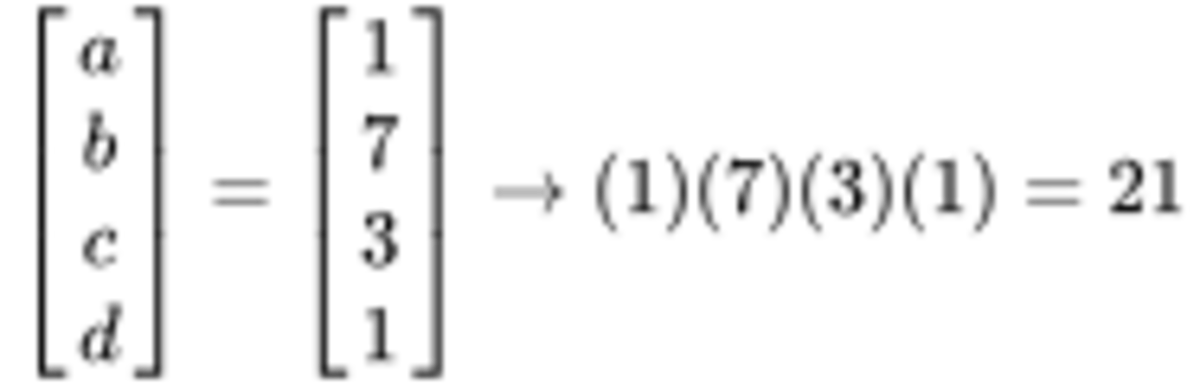
Nice to see it done using matrices, makes it look far simpler. There's an error in your third matrix. The 2 should be negative. The error wasn't carried forward though so you still got the right answer. Also in your fourth matix you did not divide your top row by -2.
Subtracting eqs. 1 & 2 will create 2d=2, which simplifies to d=1. The same can be done with eqs. 1 & 3 to find c, and so on.
a+b+c+d=12 (1)
a+b+c-d=10 (2)
a+b-c+d=-2 (3)
a-b+c+d=6 (4)
-a+b+c+d=10 (5)
(2) = (5) therefore, a=d.
(3)+(4) = 4 = 2(a+d), a+d=2, thus a=d=1
(2)+(3) = 8, 2(a+b)=8, thus b=3
plug those 3 into any eqn and you get c=7.
a.b.c.d=21
Eq1 minus eq2 same did for eq 4 & 5 and add eq3 into eq 1 get values of all elements a=1,b=3,c=7 & d=1 Now replace values in required eq = axbxcxd=1x3x7x1=21
a+b+c+d = 12 ; then :
to find d, a+b+c = 12-d
a+b+c=10+d -> 12-d = 10+d -> d=1 ;
to find c, a+b+d=12-c
a+b+d=-2+c -> 12-c = -2+c -> c=7 ;
to find b, a+c+d= 12-b
a+c+d = 6+b -> 12-b = 6+b -> b= 3;
to find a, just substitute the rest -> -a+3+7+1=10 -> a=1
abcd= 21
This sistem is impossible (2) + (3) + (4) + (5): 3(a+b+c+d)=24 >> a+b+c+d=8 (1): a+b+c+d = 12 IMPOSSIBLE!
Moderator note:
Check your working.
You didn't consider the constant values in R.H.S of equations 2,3,4,5
By adding eqns & after solving them,
We get ,a=1,b=3, c=7, d=1
Therefore, axbxcxd= 1×3×7×1=21.
if A=1, B= 3, C=7, D=1 how does A+B+C - D=10 or 1+3+7 - 1= 10?
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ a + b + c + d = 1 2 a + b + c − d = 1 0 a + b − c + d = − 2 a − b + c + d = 6 − a + b + c + d = 1 0 . . . ( 1 ) . . . ( 2 ) . . . ( 3 ) . . . ( 4 ) . . . ( 5 )
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ E q . 1 + E q . 2 : E q . 2 + E q . 3 : E q . 1 + E q . 4 : E q . 2 + E q . 3 : 2 ( a + b + c ) = 2 2 2 ( a + b ) = 8 2 ( a + c + d ) = 1 8 a + b = 4 ⇒ a + b + c = 1 1 ⇒ a + b = 4 ⇒ a + 7 + 1 = 9 ⇒ 1 + b = 4 ⇒ d = 1 ⇒ c = 7 ⇒ a = 1 ⇒ b = 3
⇒ a × b × c × d = 1 × 3 × 7 × 1 = 2 1