Just The Other Way Of Asking It
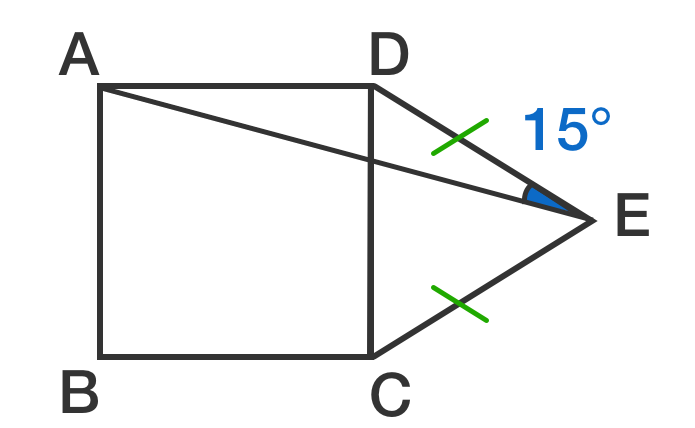
The above shows a square A B C D and a triangle C D E such that ∠ A E D = 1 5 ∘ and D E = C E . Is the triangle C D E equilateral?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Proving this is quite tough. This is the only way I found to do so:
Since we know that C E = D E , we can draw a straight line E F G which is parallel to A D , like this:
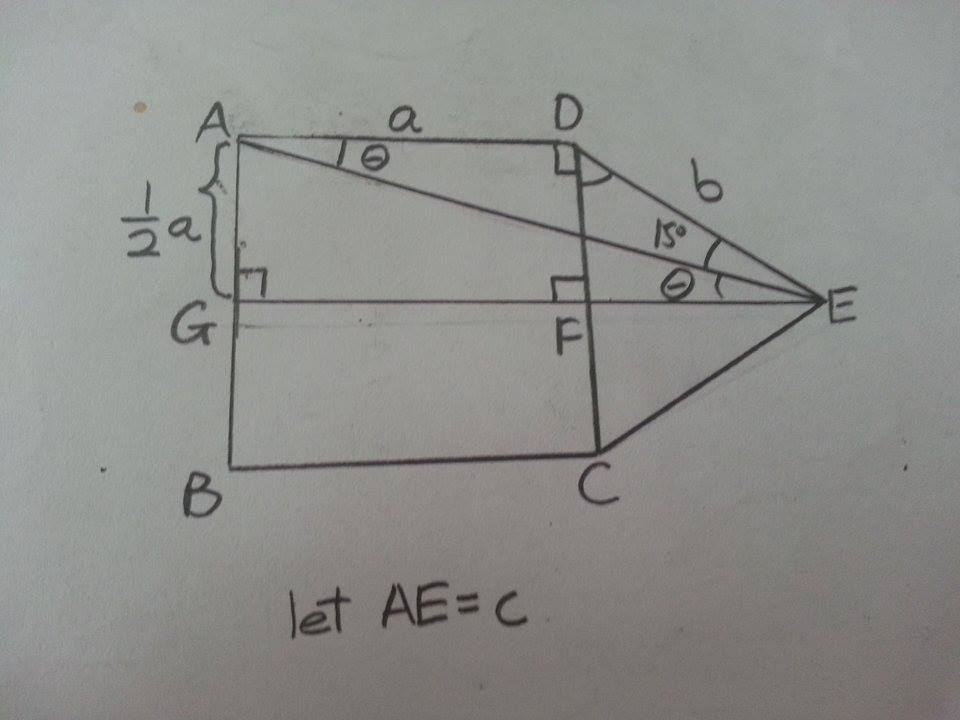
Notice that this line is also the symmetry line, line E F G divides the figure in two.
Now, let A D = a ⟹ A G = 2 a , D E = b , A E = c . From the properties of parallel lines , we know that ∠ D A E = ∠ A E G = θ
From right-angle △ A E G , we know that
sin ∠ A E G = A E A G sin θ = c 2 a a = 2 c sin θ
From △ A D E , we can use the sine rule :
sin ∠ A E D D A = sin ∠ D A E D E sin 1 5 ∘ a = sin θ b b = sin 1 5 ∘ a sin θ = sin 1 5 ∘ 2 c sin θ sin θ b = sin 1 5 ∘ 2 c sin 2 θ
sin ∠ D A E D E = sin ∠ A D E A E sin θ b = sin ( 1 8 0 ∘ − 1 5 ∘ − θ ) c sin 1 5 ∘ sin θ 2 c sin 2 θ sin θ = sin ( 1 8 0 ∘ − ( 1 5 ∘ + θ ) ) c sin 1 5 ∘ = 2 sin θ sin ( 1 5 ∘ + θ ) sin 1 5 ∘ = cos 1 5 ∘ − cos ( 1 5 ∘ + 2 θ ) cos ( 1 5 ∘ + 2 θ ) = cos 1 5 ∘ − sin 1 5 ∘ cos ( 1 5 ∘ + 2 θ ) = sin 7 5 ∘ − sin 1 5 ∘ cos ( 1 5 ∘ + 2 θ ) = sin ( 4 5 ∘ + 3 0 ∘ ) − sin ( 4 5 ∘ − 3 0 ∘ ) cos ( 1 5 ∘ + 2 θ ) = 2 cos 4 5 ∘ sin 3 0 ∘ cos ( 1 5 ∘ + 2 θ ) = 2 ( 2 1 ) ( 2 1 ) cos ( 1 5 ∘ + 2 θ ) = 2 1
Now, we know that
0 ∘ < θ < 9 0 ∘ 0 ∘ < 2 θ < 1 8 0 ∘ 1 5 ∘ < 1 5 ∘ + 2 θ < 1 9 5 ∘
Therefore, we can say that
1 5 ∘ + 2 θ = 4 5 ∘ ⟹ θ = 2 4 5 ∘ − 1 5 ∘ = 1 5 ∘
∠ D A E = ∠ A E D , therefore, △ A D E is an isosceles triangle where A D = D E
And since A D = D C , D E = E C , we know that
A D = D C = D E = E C
From this, we conclude that △ C D E is equilateral. The answer is Yes
Theorems used:
- Reference angles: 0 ∘ ≤ θ ≤ 1 8 0 ∘ , sin ( 1 8 0 ∘ − θ ) = sin θ
- Product to sum trigonometric formula : 2 sin A sin B = cos ( A − B ) − cos ( A + B )
- Complementary angles : 0 ∘ ≤ θ ≤ 9 0 ∘ , cos θ = sin ( 9 0 ∘ − θ )
- Sum to product trigonometric formula : sin ( A + B ) − sin ( A − B ) = 2 cos A sin B
@Rishabh Cool @Ashish Siva @Abhay Kumar @Chew-Seong Cheong I think my solution is too tedious for a Level 1 Geometry question...can you guys come up with a simpler solution?
Great solution! Sorry I didn't post any solution here, I just left it. Thanks for posting!
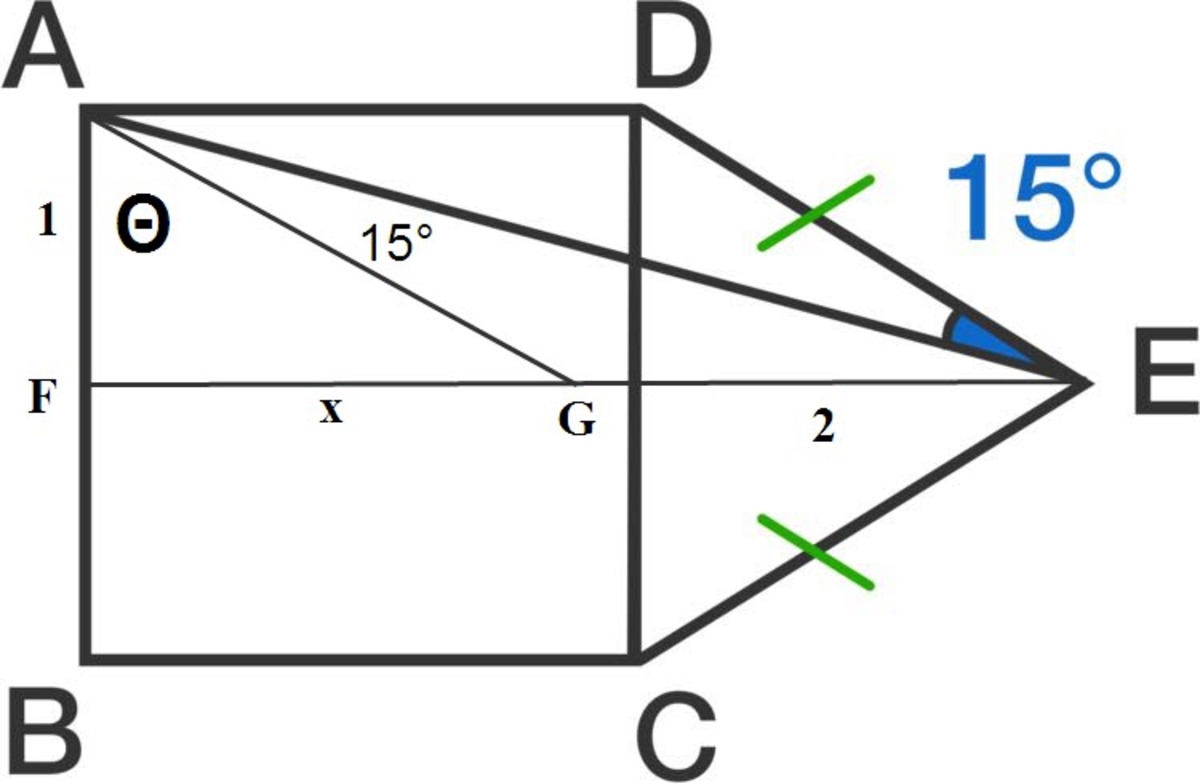 Draw FE//AD and AG // DE
Draw FE//AD and AG // DE
Let AF = 1 then GE = 2
∠EAG = 15 °
tan Θ = x , tan 15° = 2 - √3
tan (Θ + 15°) = x + 2 = 1 − x ( 2 − √ 3 ) x + ( 2 − √ 3 )
x + (2 - √3) = x(1- x (2 - √3)) + 2(1- x (2 - √3))
2 x² - √3 x² + 4x - 2√3 x - √3 = 0
(2 - √3) x² + (2 - √3) 2x - √3 = 0
x² + 2x - 3 - 2√3 = 0
x = √3
tan Θ =√3
Θ = 60°
then the triangle CDE is equilateral
Locate F on the E side of line AB such that triangle ABF is equilateral. The locus of all points G that are the vertex of a 15 degree angle AGD is an arc of the circle subtending chord AD in which angle AGD = 15 degrees can be inscribed. Since triangle ADF is isosceles and angle ADF = 150, it follows that F lies on this locus. Since F is equidistant from points C and D, it lies on the perpendicular bisector of segment CD. But point E also lies on the fore-mentioned locus and E is equidistant from points C and D, so F also lies on the perpendicular bisector of segment CD. Since the intersection of the locus arc and the perpendicular bisector of CD is unique on the E side of CD, it follows that E = F. Thus triangle CDE is equilateral.
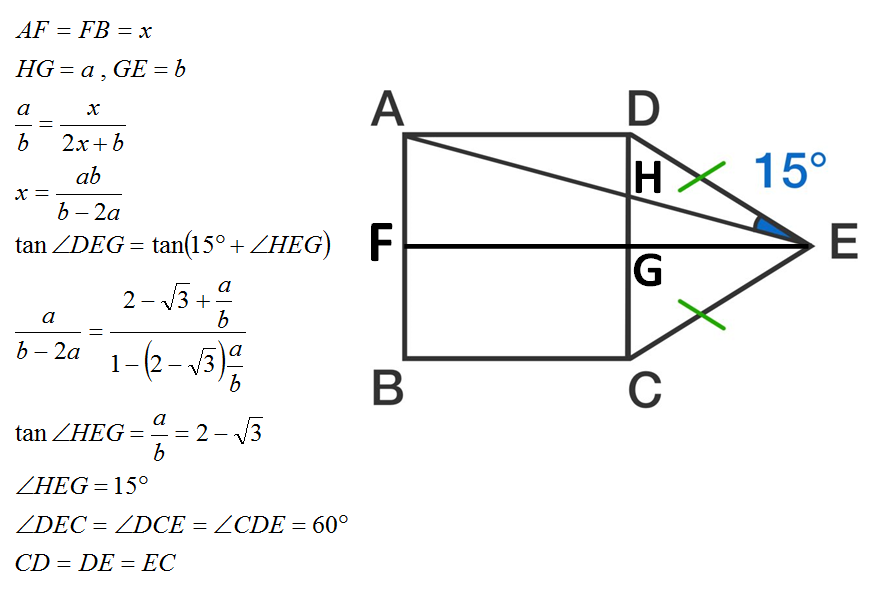
Let us assume that △ C D E is equilateral, then we check if ∠ A E D = 1 5 ∘ .
If △ C D E is equilateral, then ∠ C D E = 6 0 ∘ , D A = D E and ∠ E A D = ∠ A E D . Let ∠ A E D = θ . Then, 1 8 0 ∘ − ∠ A D E = 2 θ ⟹ 1 8 0 ∘ − 9 0 ∘ − 6 0 ∘ = 2 θ ⟹ 2 θ = 3 0 ∘ ⟹ θ = ∠ A E D = 1 5 ∘ . Therefore, if △ C D E is equilateral, ∠ A E D = 1 5 ∘ and the reverse is also true.