Easy problem to electromagnetism
Electricity and Magnetism
Level
pending
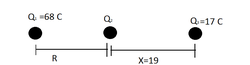In an isolated system, three Q1 particles, Q2 and Q3 loads on the horizontal axis x, are interacting with each other and Q1 and Q3 are set, the distance from Q2 to Q3 is x, find the distance from Q1 to Q2 for the system is in balance
The answer is 38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
ΣF= F3 - F1 = ma
a= 0 m/s2
F3 - F1 = 0
F3 = F1
k(Q3)(Q2)/(X^2) = k(Q1)(Q2)/(R^2)
(Q3)/(X^2) = (Q1)/(R^2)
(R^2) =(X^2)(Q1)/(Q2)
R = \sqrt{(X^2)(Q1)/(Q2)} = \sqrt{ ( (18m)^2 )( 68C ) / ( 17C ) }
R= \boxed{ 38 meters }