Eating the tasty numbers!
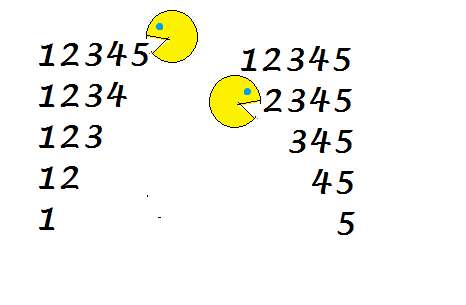 Given a positive integer
(
1
,
2
,
3
,
…
), we start
eating the number
from either left or right i.e. we start removing its digits one by one from left to right, or from right to left.
Given a positive integer
(
1
,
2
,
3
,
…
), we start
eating the number
from either left or right i.e. we start removing its digits one by one from left to right, or from right to left.
We define a set dish of the number, which is obtained by noting the number formed after eating every digit (The original number is also included) .
The taste of a number is sum of all numbers in that number's dish.
What is the smallest non-palindromic number which when eaten from left gives same taste as eating from right?
Details and Assumptions :
-
The dish of a number can be obtained in 2 ways, either eating from left or eating from right and hence there'll be 2 tastes for each number (maybe the same, that's where you count the number!)
-
Example of a dish, dish of the number 12635 as eaten from left will be { 1 2 6 3 5 , 2 6 3 5 , 6 3 5 , 3 5 , 5 } and its dish when eaten from right will be { 1 2 6 3 5 , 1 2 6 3 , 1 2 6 , 1 2 , 1 }
-
Taste of the number 123 will be 1 2 3 + 2 3 + 3 = 1 4 9 from left and it will be 1 2 3 + 1 2 + 1 = 1 3 6 from right.
-
A non-palindromic number is the one which is not the same when read from left or from right, e.g. 1 2 3 2 1 , 2 2 , 1 4 4 1 , 8 are some examples of palindromic numbers, whereas 9 8 , 2 3 4 , 2 3 9 4 7 8 are some non-palindromic numbers.
The answer is 2170.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
|
Moderator note:
You've managed to write a
java
solution that's as readable as the
python
approaches.
Thanks challenge master!
Do you have any mathematical proof for that..???
When does it stop?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
|
A pure C approach, with simultaneous testing for palindrome and taste.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Edited Shorter (but a little more obsfuscated :-) )
It's quite easy to do by lists, we just write the program to get dish using strings, this is the way I did...
1 2 3 4 5 6 7 8 9 10 11 12 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
|
Now what we do is check if the taste is same, which is just sum of the elements in lists obtained from above.
So the asked thing will be
1 2 3 4 5 6 7 8 |
|
It creates this list within a second and then see in the list, smallest non-palindromic one is 2 1 7 0
Can't you make your algorithm more efficient? See if you can understand the following:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
|
If you do write methods using lists, you can use recursion to shorten your code (a single method to return
dish
that takes two parameters, the number and the direction of eating).
1 2 3 4 |
|
... and then define a method
equal_taste()
as,
1 |
|
The general conditions on the digits of an (n+1)-digit number $x 0 \dots x n$ is left taste = right taste, ie. ∑ k = 0 n k ⋅ 1 0 n − k x k = ∑ k = 0 n x k ∑ j = 0 n − k 1 0 j . For n=0, the number is trivially palindromic. For n=1, we obtain 1 0 x 0 + 2 x 1 = 1 1 x 0 + x 1 , which reduces to x 0 − x 1 = 0 so any 2-digit solution must also be palindromic. For n=2, we need 1 1 1 x 0 + 1 1 x 1 + x 2 = 1 0 0 x 0 + 2 0 x 1 + 3 x 2 , which requires 1 1 x 0 − 9 x 1 − 2 x 2 . This has nonpalindromic solutions, but only when one of the digits is larger than 9, which is also forbidden. So we need to consider n=3. Here we have 1 1 1 1 x 0 + 1 1 1 x 1 + 1 1 x 2 + x 3 = 1 0 0 0 x 0 + 2 0 0 x 1 + 3 0 x 2 + 4 x 3 , whereby we obtain 1 1 1 x 0 − 8 9 x 1 − 1 9 x 2 − 3 x 3 . Finally, after a little testing a nontrivial solution can be found by x 0 = 2 , x 1 = 1 , x 2 = 7 , x 3 = 0 .
A perl solution. Could probably be made 'nicer'
sub ftaste {
(my $num) = @_;
my $taste = 0;
my $length = length $num;
for (my $x=0;$x<$length;$x++) {
$taste += substr ($num, $x);
}
return $taste;
}
sub rtaste {
(my $num) = @_;
my $taste = 0;
my $length = length $num;
for (my $x=1;$x<=$length;$x++) {
$taste += substr ($num, 0, $x);
}
return $taste;
}
my $natural = 1;
my $found = 0;
while ( $found == 0 ) {
if ( $natural != reverse $natural and ftaste($natural) == rtaste($natural) ) {
$found = 1;
}
else {
$natural ++;
}
}
print "Smallest non palindromic natural number with equal tastes is $natural\n";
Removing its digits one by one can be done mathematically, but python's
string
library is more convenient and provide more readability. Thus, I implemented all three functions below with first taking in an
int
parameter then convert it to a
string
. Look how intuitive it got after that!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
No effort expended for efficiency, yet it provides the answer quickly.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
This is my solution in python
def Dish(N):
D=[]
sumM1=0
sumM2=0
for i in str(N):
D.append(int(i))
check=0
for i in range(1,len(D)+1):
n=len(D)-(i-1)
M1=( D[n-1] * (n))
M2=sum(D[i] for i in range(0,n))
sumM1=sumM1 + (M1 * (10** (i-1)))
sumM2=sumM2 + (M2 * (10** (i-1)))
if sumM1 ==sumM2:
return True
for N in range(1000,10000):
if Dish(N):
print N
Looking at the numbers printed by the above code ,We can easily see the first non-palindrome which is 1 2 7 0 .
If someone wants a C++ solution, here's mine:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
|
Brute force is sufficient to solve this problem. Here's is my Java code for this problem :-
- boolean check(int num){
- String x = Integer.toString(num);
- if(x.equals(new StringBuilder(x).reverse().toString())) return false;
- int gum = Integer.parseInt(x);
- int sum = Integer.parseInt(x);
- for(int i=1;i<x.length();i++){
- gum += Integer.parseInt(x.substring(i,x.length()));
- sum += Integer.parseInt(x.substring(0, x.length()-i));
- }
- if(gum == sum) return true;
- else return false;
- }
Python 2.7: