Edge effects in the parallel plate capacitor.

Electricity and Magnetism Level 5

As we know, the simplest capacitor, consists of two conductive plates separated by air (or any other dielectric). If the surface charge density of the plates are $\pm \sigma$ then we know that there is a homogeneous electric field between the plates given by $E=\frac{\sigma}{\epsilon_{0}}$ However, this simple expression for the electric field only works when the dimensions of the plates are much greater than its separation. In addition, the above formula only describes the field correctly at points which are far from the edges of the capacitor. Far from the center of the capacitor, the so-called "edge effects" play an important role and the magnitude of the electric field deviates from $\frac{\sigma}{\epsilon_{0}}$ . In order to verify this, determine the magnitude of the electric field in volts per meter at a point P located at the corner of the capacitor and right between the plates. The surface charge density of the plates is $\sigma= 1~\mbox{nC/m}^{2}$ .

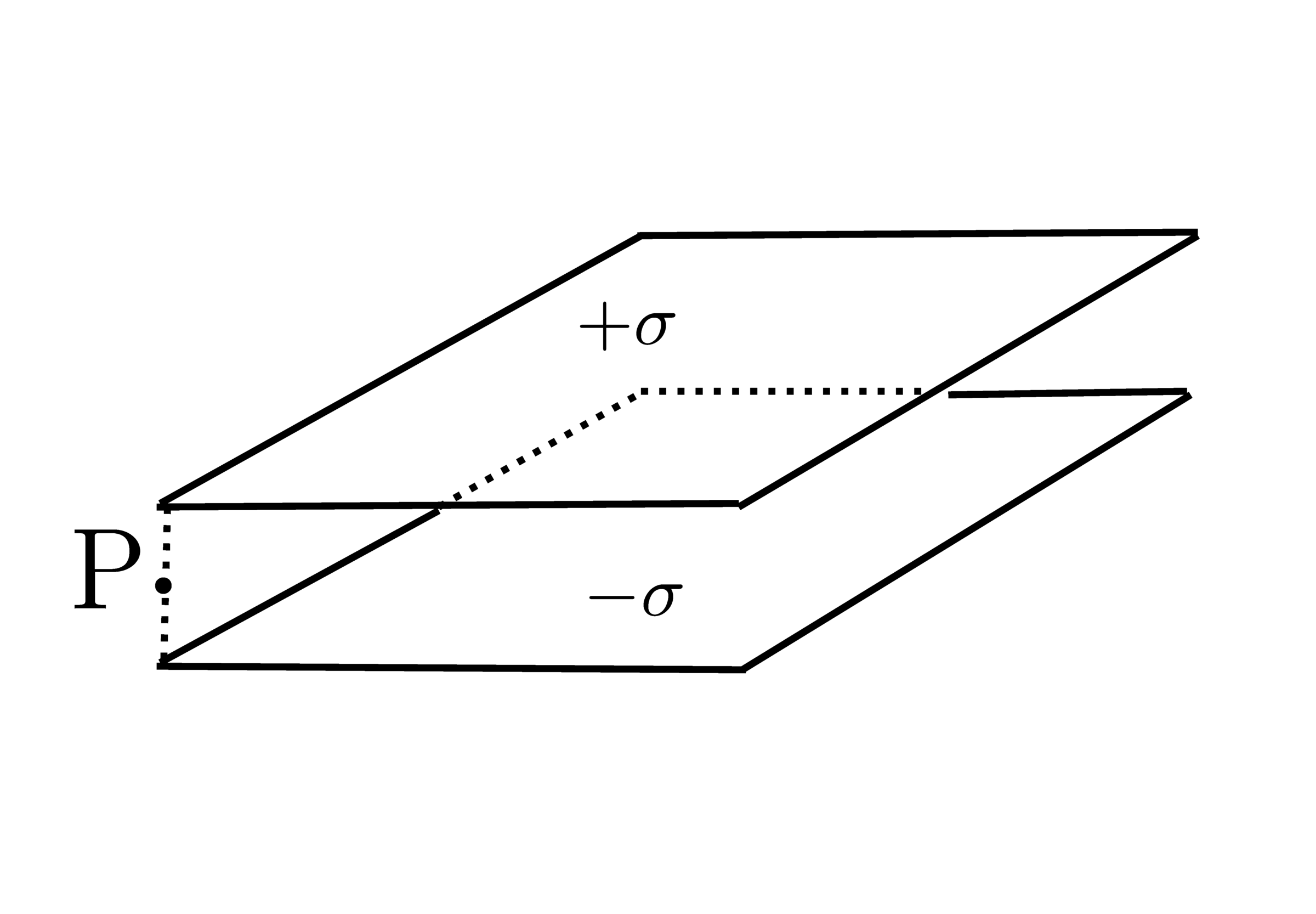
Details and assumptions

$\epsilon_{0}=8.85\times 10^{-12}~\mbox{F}\cdot \mbox{m}^{-1}$

The answer is 28.25.

5 solutions

Maharnab Mitra
Oct 13, 2013

Consider the two plate system as a whole unit. If there were four such units around point P, P would have been the centre of the new bigger capacitor and the electric field at P would have been $\frac{\sigma}{\epsilon_o}$ . As there is only one part present, electric field at P is reduced to $\frac{\sigma}{4 \epsilon_o}$ . Putting in the corresponding values, we get the answer as $28.25Vm^{-1}$ .

Didn't think about this. After thinking that Gauss law is impossible to use, I started integrating. But the integral became too hard so I left it!

Snehal Shekatkar - 7 years, 7 months ago

What will be the electric field at point P if that is two parallel circular plates?

Anjishnu Adhikari - 5 years ago

How will you guarantee that electric field will have no components parallel to plate? If you prove that, then it's fine.

Ananjan Nandi - 2 years, 4 months ago

@Ananjan Nandi right

Danish Javed - 2 years, 2 months ago

Devansh Agrawal
Oct 18, 2013

This question is very simple.

Notice that at position P, if it were an infinite plate, there would be 3 more pairs of plates around it (in the 3 other quadrants)

Since it is all symmetric, the E field currently is only produced by a quarter of the infinite plate, thus it is simply

$\frac{\sigma}{4*\epsilon} = 28.249 V \cdot m^{-2}$

Akash Yadav
Jul 2, 2017

Question would have been made more interesting if we would have allowed the charged particle to oscillate by displacing it tiny bit downwards and finding out time period But for that we need dimensions of the plate.

Rohan Singh
Oct 14, 2013

if area of plates is A , consider a capacitor with plate area 4A (by adding 3 same capacitors on the side of existing capacitor to make a capacitor with similar shape as original but 4A area) and same surface charge density

the field at the center (which is corner of original) can be considered to be equally contributed by all the 4(A area) plates(by symmetry). therefore field=σ/ϵ=4*field due to one capacitor

so, field at P=σ/4ϵ=28.25

Prabhanjan Mannari
Oct 13, 2013

Consider the system given to be 1/4 th of a whole system made up of 4 such plates. The field at P is given by (sigma/epsilon knot). This is due to 4 such plates. Hence due to a single plate the field is (sigma/4epsilon knot)= 28.25

Edge effects in the parallel plate capacitor.

The answer is 28.25.

5 solutions

1 pending report

Vote up reports you agree with