Efficient Archiving

Solution 1

The other possible coding schemes with the same order of frequencies are as follows:

Scheme II: $\begin{array}{llll} \text{instruction} & \text{frequency} & \text{bit string} & \\ \hline \mathbf{auto} & x & \mathtt{0} & \text{1 bit} \\ \mathbf{check} & y & \mathtt{110} & \text{3 bits} \\ \mathbf{op1} & z & \mathtt{111} & \text{3 bits} \\ \mathbf{op2} & z & \mathtt{100} & \text{3 bits} \\ \mathbf{op3} & z & \mathtt{101} & \text{3 bits} \\ \hline \end{array}$

Scheme III: $\begin{array}{llll} \text{instruction} & \text{frequency} & \text{bit string} & \\ \hline \mathbf{auto} & x & \mathtt{0} & \text{1 bit} \\ \mathbf{check} & y & \mathtt{10} & \text{2 bits} \\ \mathbf{op1} & z & \mathtt{110} & \text{3 bits} \\ \mathbf{op2} & z & \mathtt{1110} & \text{4 bits} \\ \mathbf{op3} & z & \mathtt{1111} & \text{4 bits} \\ \hline \end{array}$

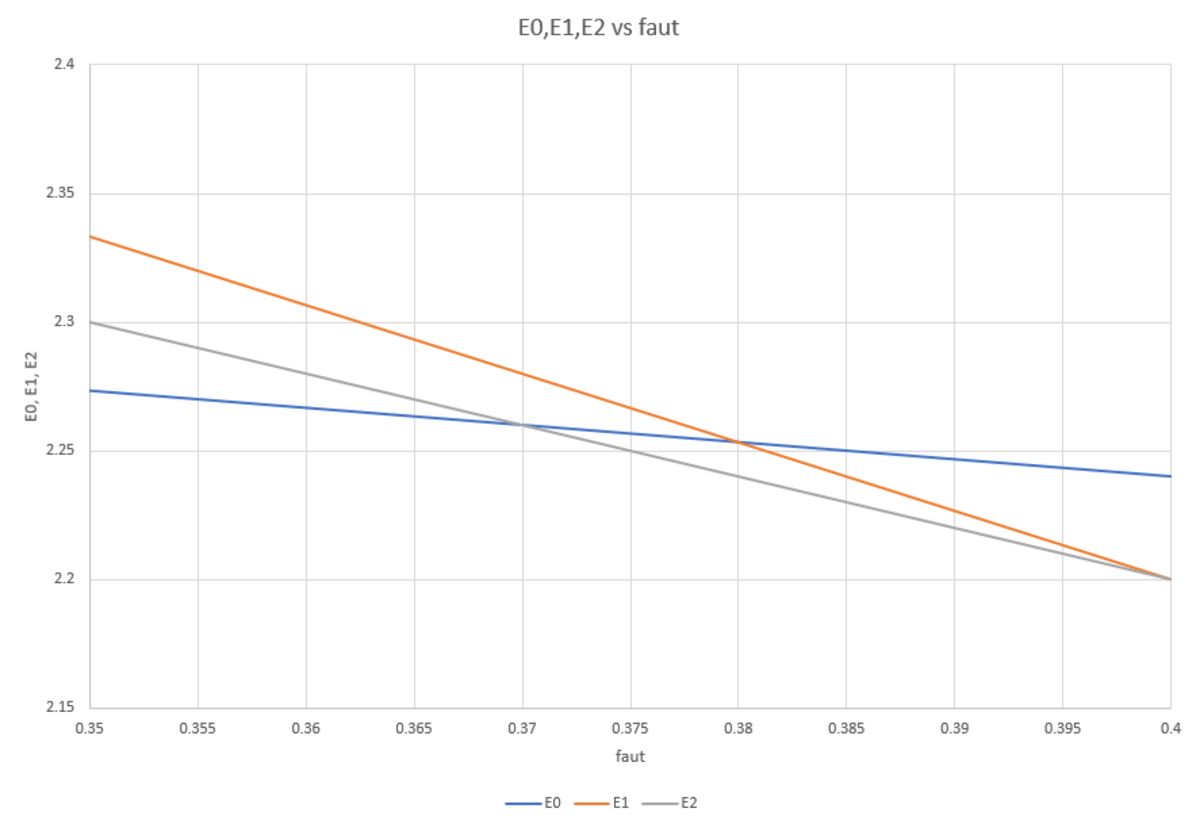
We have $y = 0.24$ , and $z = \tfrac13(0.76 - x)$ ; the expected bit string length for each of the schemes is: $\begin{cases} n_I = 2x + 2y + 8z = \tfrac13(7.52 - 2x) & \text{for scheme I (current code)} \\ n_{II} = x + 3y + 9z = 3.00 - 2x & \text{for scheme II} \\ n_{III} = x + 2y + 11z = \tfrac13(9.80 - 8x) & \text{for scheme III} \end{cases}$

Now $n_{II} < n_I$ iff $x > 0.37$ ; and $n_{III} < n_I$ if $x > 0.38$ . Therefore it is efficient to switch to scheme II as soon as the percentage of $\mathbf{auto}$ increases beyond $\boxed{37}\%$ . (Note: for values over $40\%$ , it is more efficient to switch to scheme III.)

$\begin{array}{r|rrrrrrrr} x & 34\% & 35\% & 36\% & 37\% & 38\% & 39\% & 40\% & 41\% \\ \hline n_{I} & 2.280 & 2.273 & 2.267 & 2.260 & 2.253 & 2.247 & 2.240 & 2.233 \\ n_{II} & 2.320 & 2.30 & 2.280 & 2.260 & 2.240 & 2.220 & 2.200 & 2.180 \\ n_{III} & 2.360 & 2.333 & 2.307 & 2.280 & 2.253 & 2.227 & 2.200 & 2.173 \\ \hline \end{array}$

---

Solution 2

The most efficient bit string code is generated by the Huffman algorithm . We will apply this algorithm to the original values and reconstruct the given bit code; but we also keep track of the conditions under which the algorithm changes.

This algorithm tells us to "lump together" the elements with the lowest frequencies, and to repeat this process until a coding "tree" is built. In our case, we start out with the following elements and frequencies: $\mathbf{auto}:\ 34\%+3\delta;\ \ \ \mathbf{check}:\ 24\%;\ \ \ \mathbf{op1}:\ 14\%-\delta;\ \ \ \mathbf{op2}:\ 14\%-\delta;\ \ \ \mathbf{op3}:\ 14\%-\delta.$

The first step of the algorithm combines the instructions $\mathbf{op2}$ and $\mathbf{op3}$ : $\mathbf{auto}:\ 34\%+3\delta;\ \ \ \mathbf{check}:\ 24\%;\ \ \ \mathbf{op1}:\ 14\%-\delta;\ \ \ [\mathbf{op2},\mathbf{op3}]:\ 28\%-2\delta.$ Second step: Now the lowest frequencies are those of $\mathbf{check}$ and $\mathbf{op1}$ , so they will be combined next. However , this choice will change if the combined frequency of $\mathbf{op2}$ and $\mathbf{op3}$ becomes less than 24\%. The Huffman code will change its behavior if $\delta > 2$ . $\mathbf{auto}:\ 34\%+3\delta;\ \ \ [\mathbf{check}, \mathbf{op1}]:\ 38\%-\delta;\ \ \ [\mathbf{op2},\mathbf{op3}]:\ 28\%-2\delta.$

Third step: Now the lowest frequencies are those of $\mathbf{auto}$ and $[\mathbf{op2},\mathbf{op3}]$ . Therefore they will be combined next. However , this choice changes if the frequency of $\mathbf{auto}$ becomes greater than that of $[\mathbf{check}, \mathbf{op1}]$ . We solve $34+3\delta = 38-\delta$ to find that this will be the case when $\delta = 1$ . The Huffman code will change its behavior if $\delta > 1$ . $[\mathbf{check}, \mathbf{op1}]:\ 38\%-\delta;\ \ \ [\mathbf{auto},[\mathbf{op2},\mathbf{op3}]]:\ 62\%+\delta.$

Fourth step: The last two elements are combined. $[[\mathbf{auto},[\mathbf{op2},\mathbf{op3}]],[\mathbf{check}, \mathbf{op1}]]:\ 100\%.$ From this nested list one can read off the bit code: register "0" for the left element, "1" for the right element.

In the analysis above, we saw that the Huffman code changes first when $\delta$ becomes greater than one; this means that the frequency of $\mathbf{auto}$ has become $\boxed{37}\%$ . The result will be $[\mathbf{auto},[[\mathbf{op2},\mathbf{op3}],[\mathbf{check}, \mathbf{op1}]]].$ This corresponds to what we called "Scheme II" under Solution 1 above.

---

Further analysis

Here is a graphical analysis of bit codes for an alphabet with a symbol of frequency $x$ , a symbol of frequency $y$ , and three symbols of equal frequency $\tfrac13 z$ .

The Roman numerals represent the various optimal codes:

• Code I : $x, y, z_1$ : 2 bits; $z_2,z_3$ : 3 bits.

• Code II : $x$ : 1 bit; $y, z_1, z_2, z_3$ : 3 bits.

• Code III : $x$ : 1 bit; $y$ : 2 bits; $z_1$ : 3 bits; $z_2, z_3$ : 4 bits.

• Code IV : $x,z_1,z_2$ : 2 bits; $y,z_3$ : 3 bits.

• Code V : $z_1,z_2,z_3$ ; 2 bits; $x,y$ : 3 bits.

(In codes II , III , _ IV , swap $x$ and $y$ for the right side of the diagram.)

The expected number of bits per character may be read off using the red lines/numerals.

The following detail shows the particular situation of this problem, where the frequency of $x$ increases from $34\%$ , while the frequency of $y$ remains constant at $24\%$ :

Follow the purple arrow to see how with increasing $x$ , the code changes from I to II to III .

This solution is nowhere near as comprehensive as Arjen's, but here it is anyway. As "auto" becomes more and more frequent, the natural evolution of the code is to move the "auto" symbol to a single bit, and increase the bit lengths for the other symbols. The trick is to preserve the unique decode-ability in the process. I looked online for some 5-symbol Huffman codes, and ended up evaluating the following codes (specified in terms of the number of bits for each symbol):

Standard code presented in the problem: (2,2,2,3,3)
Alternate code 1: (1,2,3,4,4)
Alternate code 2: (1,3,3,3,3)

Code to evaluate the performance as we ramp down "fop", and correspondingly ramp up "faut". (E0,E1,E2) are expected bits per instruction for the three codes.

fchk = 0.24

fop = 0.14              # sweep fop downwards
dfop = 10.0**(-4.0)

print "faut E0 E1 E2"


while fop > 0.0:

    faut = 1.0 - fchk - 3.0*fop

    E0 = 2.0*faut + 2.0*fchk + 2.0*fop + 3.0*fop + 3.0*fop
    E1 = 1.0*faut + 2.0*fchk + 3.0*fop + 4.0*fop + 4.0*fop
    E2 = 1.0*faut + 3.0*fchk + 3.0*fop + 3.0*fop + 3.0*fop

    print faut,E0,E1,E2


    fop = fop - dfop

Graph of expected instruction length vs. "faut", for all three codes. The graph indicates that E0 is only minimum up until "faut" reaches 37%.