Efficient Mowing
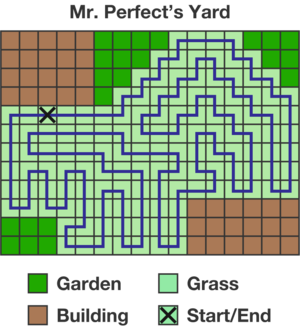
Mr. Perfect can mow his lawn efficiently, that is, he can mow his whole lawn in a continuous line from start to finish without having to go over an already mown part, as shown by the blue path below.
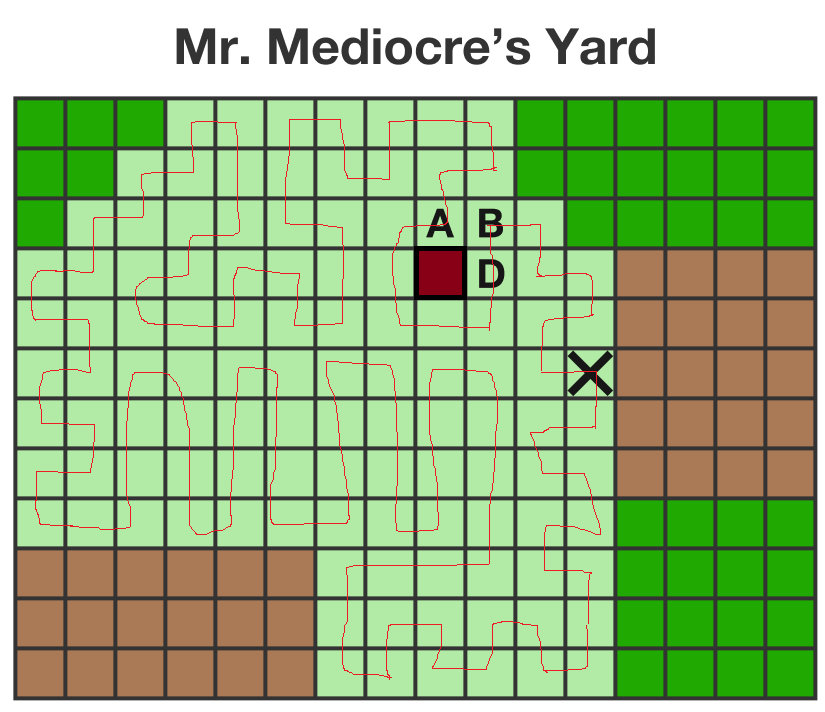
No matter how hard he tries, Mr. Mediocre cannot mow his lawn (shown below) as efficiently as Mr. Perfect can. A friend suggests that Mr. Mediocre plant a shrub somewhere to change the layout of his yard.
Where should Mr. Mediocre plant the shrub so that he can mow his lawn efficiently?

Assumptions:
- The lawnmower can only move straight through a square or make one right angle in the square.
- The lawnmower cannot move diagonally between squares.
- After the lawnmower enters and exits a square, all of the grass in the square is cut.
Bonus: Prove that before he plants the shrub, it is impossible for Mr. Mediocre to mow his lawn efficiently.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
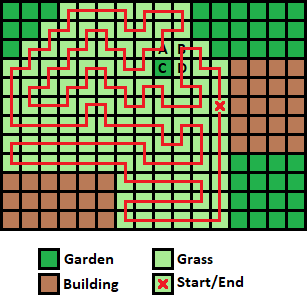
Begin with a parity argument. I shaded 57 squares black and left the other 58 green. Any complete circuit must have the same number of black and green because the path must alternate between black and green squares and end where it begins. (This takes care of the bonus.)
So we must get rid of a green square to have a chance at a possible lawn. That rules out A and D.
That square cannot be B because the square directly to the right of it would be a dead end.
This leaves the only possibility C .
(I was able to find a solution on graph paper.)