Egyptian fraction of a unit fraction
If a and b are distinct positive integers satisfying 3 1 = a 1 + b 1 , find a + b .
Bonus : Generalize it for any unit fraction c 1 , where c is a positive integer.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
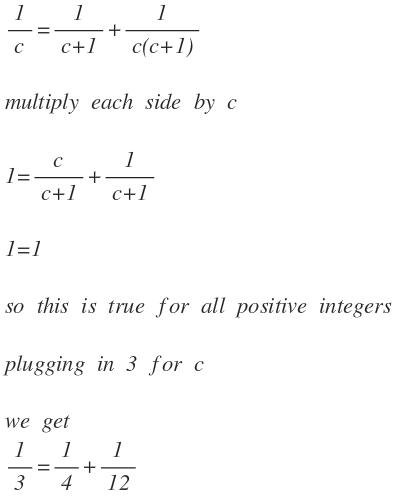
4+12=16
Note:If c isn't prime,then it will have other possible solutions
Log in to reply
i was doing a summation problem (telescoping sum) which was the sum of 1/n(n+1)
you know this is equal to (1/n) - 1/(n+1) i added 1/(n+1) to both sides and got
n 1 = n + 1 1 + n ( n + 1 ) 1
Clearly, a , b > c If we set, a = c + x , b = c + y for some integers x , y > 0 , the equation becomes, c 1 = c + x 1 + c + y 1 Simplifying, we have, ( c + x ) ( c + y ) = c ( 2 c + x + y ) This becomes, c 2 = x y In general, x + y cannot be unique unless c = p for some prime p , giving, x = p 2 , y = 1 as x = y .
Then we have, a = c 2 + c , b = c + 1 Here, c = 3 , so a + b = 1 2 + 4 = 1 6