Eigenman's problem I-15
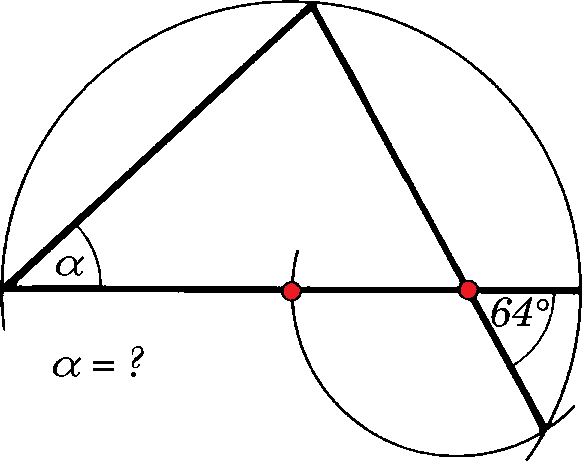
Find α in degrees.
Notes: The two red points denote the centers of the two partially drawn circles.
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
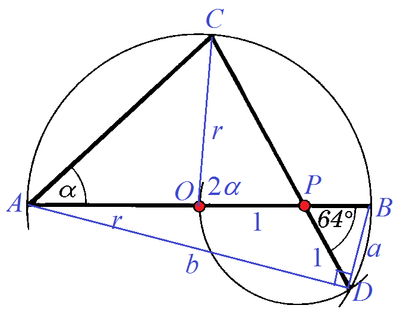 Let the radii of the small circle and big circle be 1 and
r
respectively. Since
A
B
is a diameter,
∠
A
D
B
=
9
0
∘
. Let
B
D
=
a
and
A
D
=
b
. Then by
cosine rule
, we have:
Let the radii of the small circle and big circle be 1 and
r
respectively. Since
A
B
is a diameter,
∠
A
D
B
=
9
0
∘
. Let
B
D
=
a
and
A
D
=
b
. Then by
cosine rule
, we have:
{ a 2 = ( r − 1 ) 2 + 1 − 2 ( r − 1 ) cos 6 4 ∘ b 2 = ( r + 1 ) 2 + 1 + 2 ( r + 1 ) cos 6 4 ∘ . . . ( 1 ) . . . ( 2 ) Note that cos ( 1 8 0 ∘ − θ ) = − cos θ
By Pythagorean theorem , a 2 + b 2 = ( 2 r ) 2 :
( 1 ) + ( 2 ) : 4 r 2 r 2 ⟹ r = 2 r 2 + 2 + 2 + 4 cos 6 4 ∘ = 2 ( 1 + cos 6 4 ∘ ) = 2 ( 1 + 2 cos 2 3 2 ∘ − 1 ) = 2 cos 3 2 ∘
Now we note that ∠ C O P = 2 α and ∠ O C P = 1 8 0 ∘ − 6 4 ∘ − 2 α = 1 1 6 ∘ − 2 α . By sine rule :
1 sin ( 1 1 6 ∘ − 2 α ) sin ( 6 4 ∘ + 2 α ) 2 sin ( 3 2 ∘ + α ) cos ( 3 2 ∘ + α ) cos ( 5 8 ∘ − α ) cos ( 3 2 ∘ + α ) cos ( 2 α − 2 6 ∘ ) + cos 9 0 ∘ cos ( 2 α − 2 6 ∘ ) ⟹ 2 α − 2 6 ∘ α = r sin 6 4 ∘ = cos 3 2 ∘ sin 6 4 ∘ = cos 3 2 ∘ 2 sin 3 2 ∘ cos 3 2 ∘ = cos 5 8 ∘ = cos 5 8 ∘ = cos 5 8 ∘ = 5 8 ∘ = 4 2 ∘ Note that sin ( 1 8 0 ∘ − θ ) = sin θ And r = cos 3 2 ∘
Follow the angles, using the isoceles triangles in this figure
Angle α is equal to 9 0 − 4 3 β , where β = 6 4 for this problem