Eight squares painted on a flag

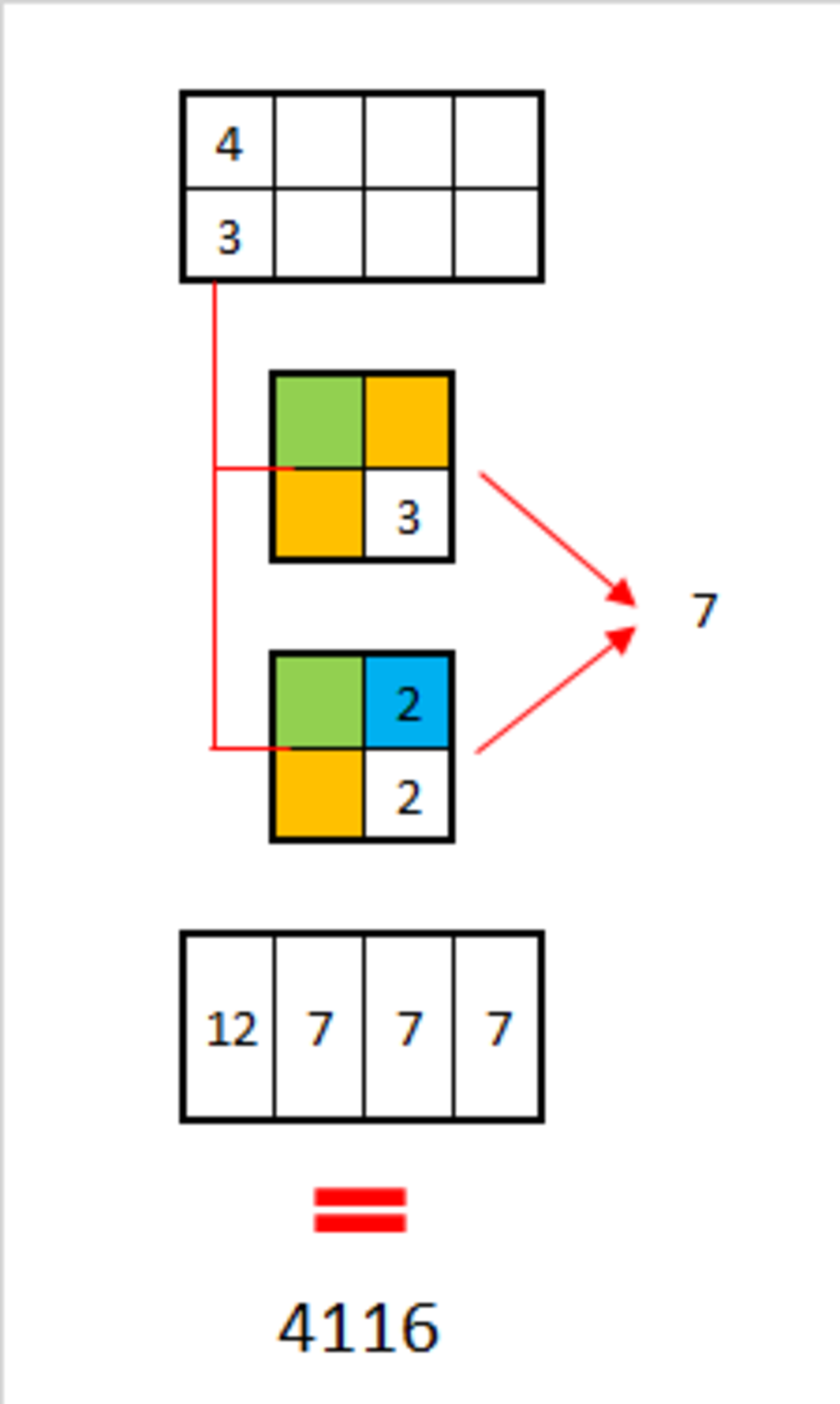
First column can be painted of $4\times3=12$ ways. Then exist two cases for paint the second column:

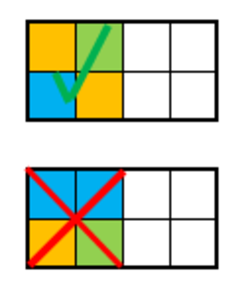
$1)$ diagonal's squares are of the same color $\Rightarrow 3$ ways

$2)$ diagonal's squares are of different color $\Rightarrow 4$ ways

This apply for the next two columns $\therefore$ are $12\times 7^3=\boxed{4116}$ ways of paint it