Eight Strings
Eight pieces of string lie side by side on a table.
You tie the top ends of the strings together into four random pairs, and then do the same for the bottom ends.
What is the probability (as a decimal) that all of the strings have been tied into one single loop?
The answer is 0.45714285714.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
I solved it in a similar way. In the beginning I complicated things. I thought it is related to dearangements.
there is a typo in your decimal representation in the box
I get what you're going for, but this could be clearer.
"The top ends don't matter." By symmetry, the bottom ends don't matter!
I would rephrase it along the lines of "First, let us randomly tie the knots at the top. This will yield four distinct, unconnected strings..."
Log in to reply
That the tops are tied first is already stated in the problem, but I will clarify.
I forgot we had already tied some of the ends together, and got it wrong😢, anyway good answer
Log in to reply
I did the same thing. My question is, why is that wrong? It never says we can't tie a string to a string it is already tied to, just that it is attached to a 'random other string.'
Can this be extended to 2n strings on the table
Tie the top ends together however you like.
Once this is done, the number of ways the bottom ends can be tied together is 7 ⋅ 5 ⋅ 3 ⋅ 1 = 1 0 5
The number of ways that result in a loop is: 6 ⋅ 4 ⋅ 2 ⋅ 1 = 4 8
1 0 5 4 8 = 0 . 4 5 7
@Geoff Pilling how do u solve for the loop part?can u give extra explanation
Log in to reply
Well, once you have tied the top ones together, you need to tie the bottom ones together such that they form a loop.
If you grab one (of the eight) ends at random you can tie it to six of the remaining seven ends and still make a large loop.
Now if you consider another end of the one you just tied, you have 4 possibilities, and so on...
Giving you 6 ⋅ 4 ⋅ 2 total possibilities. The one isn't really needed since there is only one way to tie the remaining two together.
See Jeremy's explanations above. It's a bit more thorough.
Another way of looking at Geoff's explanation: Tie the tops of the strings together any way. Now tie a bottom end to one of the other ends. There are 7 ends to choose from. Do not choose the string already connected at the top. The probability of choosing suitably is 6/7. Continue in this way. The probabilities that the other three knots are tied suitably are 4/5, 2/3 and 1/1. Combined probability: 6/7.4/5.2/3 = 0.457.
That's how I did it.
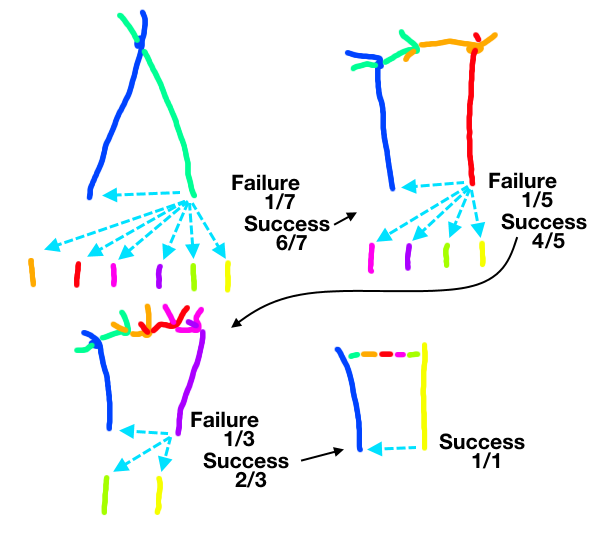 7
6
×
5
4
×
3
2
×
1
1
=
1
0
5
4
8
≈
0
.
4
5
7
7
6
×
5
4
×
3
2
×
1
1
=
1
0
5
4
8
≈
0
.
4
5
7
this is the only explaination that made sense to me. A picture really is worth a thousand words.
Suppose we matched threads (ab) (cd) (ef) (gh) at the top, but of course we do not know which is which.
Start with any thread (say it is a) connect it to another one. Only b is wrong, so 6 out of 7 belong to a new pair, say it is c. At some point, we will connect d. 4 out of 5 belong to a new pair. If we do that right (say we chose e), we have to match f. 2 out of 3 are right. Now connecting the remaining 2 threads completes the circle. Altogether we have probability 7 6 5 4 3 2 = 1 0 5 4 8 to do it right
I started by labeling 8 strings A through H. Pair them as AB, CD, EF, GH.
Start by tying A to any of the 7 other strings. You have reduced your 8 untied strings to 6. Choose any untied string, there are 5 choices to tie it to. You are left with 4 untied strings. Choose one, there are 3 choices of untied strings. Your last 2 untied strings must be tied together. Total choices are 7 × 5 × 3 × 1 = 1 0 5
Which choices create only one loop?
Start with A. You cannot tie A to its partner B, but any of the other 6 will be OK. Call your choice C.
B cannot be tied to D, C's partner, otherwise we create a loop of 4 string segments, but any of the other 4 will be OK. Call your choice E.
D cannot be tied to F, E's partner, otherwise we create a loop of 6 string segments. D must tie to G or H. F ties to the other one.
6 × 4 × 2 × 1 = 4 8
4 8 / 1 0 5 = 0 . 4 5 7 1 4 . . .
The solution can be easily found out for k number of strings by using the general expression (k-1)! / {(k-1)!!}^2 i.e factorial of one less than k , k-1 divided by square of DOUBLE factorial of one less than k, k-1.
For the given question, k is 8 Probability of single loop =(8-1)!/ ( (8-1)!!)^2
= 7! / (7!! X 7!!)
Now 7! = 5040 and 7 !! = 7x (7-2) X(5-2) x(3-2)= 105
So it is 5040 / (105 x105)
= 0.457142857
Once the top ends are joined, there are:
7×5×3×1=105
ways to join the lower ends.
To find the number of favourable cases, fix one loop and its orientation, for example in the figure of the loop in the question, fix the top left loop alongwith its orientation.
Then there are 3!=6 ways to arrange the three other loops and 2 ways each to orient them.
Therefore, 6×2×2×2=48 favourable cases.
Probablity=48/105=16/35=0.4571...
The Answer can be extended to 2n strings to show that the probability that the pieces of string are all joined in one loop is
(2n-1)!/[(2n-1)!!]^2
For n=4,
Answer=16/35=0.4571
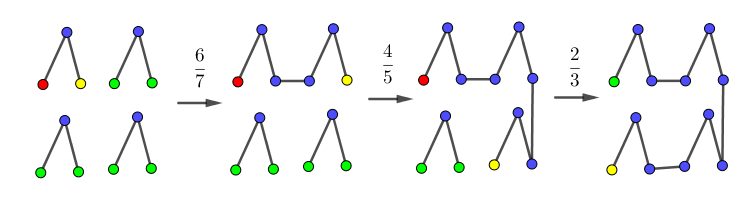 Blue
=
completed node.
Blue
=
completed node.
Yellow
=
current node.
Green
=
valid node to connect to.
Red
=
invalid node to connect to.
The fractions are the probabilities that the yellow node will connect to a green node, so the total probability for a single loop is 7 6 ⋅ 5 4 ⋅ 3 2 = 3 5 1 6 ≈ 0 . 4 5 7 1 4 2 8 5 7 1 4 .
As they are tied first, the top ends don't matter, the result of tying them in any order will be 4 single strings, each with 2 ends.
Choose one end of a string. There are 7 other ends, of which 6 are ok to tie it to (the 7th would result in a single loop.)
You can consider what you have now as 3 single strings.
Choose one end of a string. There are 5 other ends, of which 4 are ok to tie it to (the 5th would result in a single loop.)
You can consider what you have now as 2 single strings.
Choose one end of a string. There are 3 other ends, of which 2 are ok to tie it to (the 3rd would result in a single loop.)
You can consider what you have now as 1 single string. Go ahead and tie it.
Total probability: 7 6 ⋅ 5 4 ⋅ 3 2 = 1 0 5 4 8 ≈ 0 . 4 5 7 1 4 2 8 5 7 1