Eisensteins Everywhere

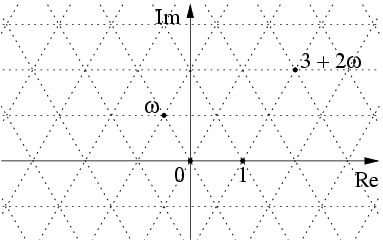
Looking at a random direction from the origin, what is the probability that your line of sight doesn't encounter an Eisenstein integer (that is, the probability that a line from the origin at a random direction does not intersect any Eisenstein integer)?

If the probability is $P,$ submit your answer as $\lfloor 1000P \rfloor$ .

Notes:

• An Eisenstein integer is a complex number of the form $a+b\omega,$ where $\displaystyle \omega = \frac{-1+i\sqrt{3}}{2}$ and $a$ and $b$ are both integers. For example, $1, \omega$ and $3+2\omega$ are all Eisenstein integers.

• $\lfloor \cdot \rfloor$ denotes the floor function .

---

Inspiration .