Electric and Magnetic Fields
A particle of mass
and charge
is placed at
is at rest and free to move . There is a constant and uniform electric field
and a constant and uniform magnetic field is applied at
.
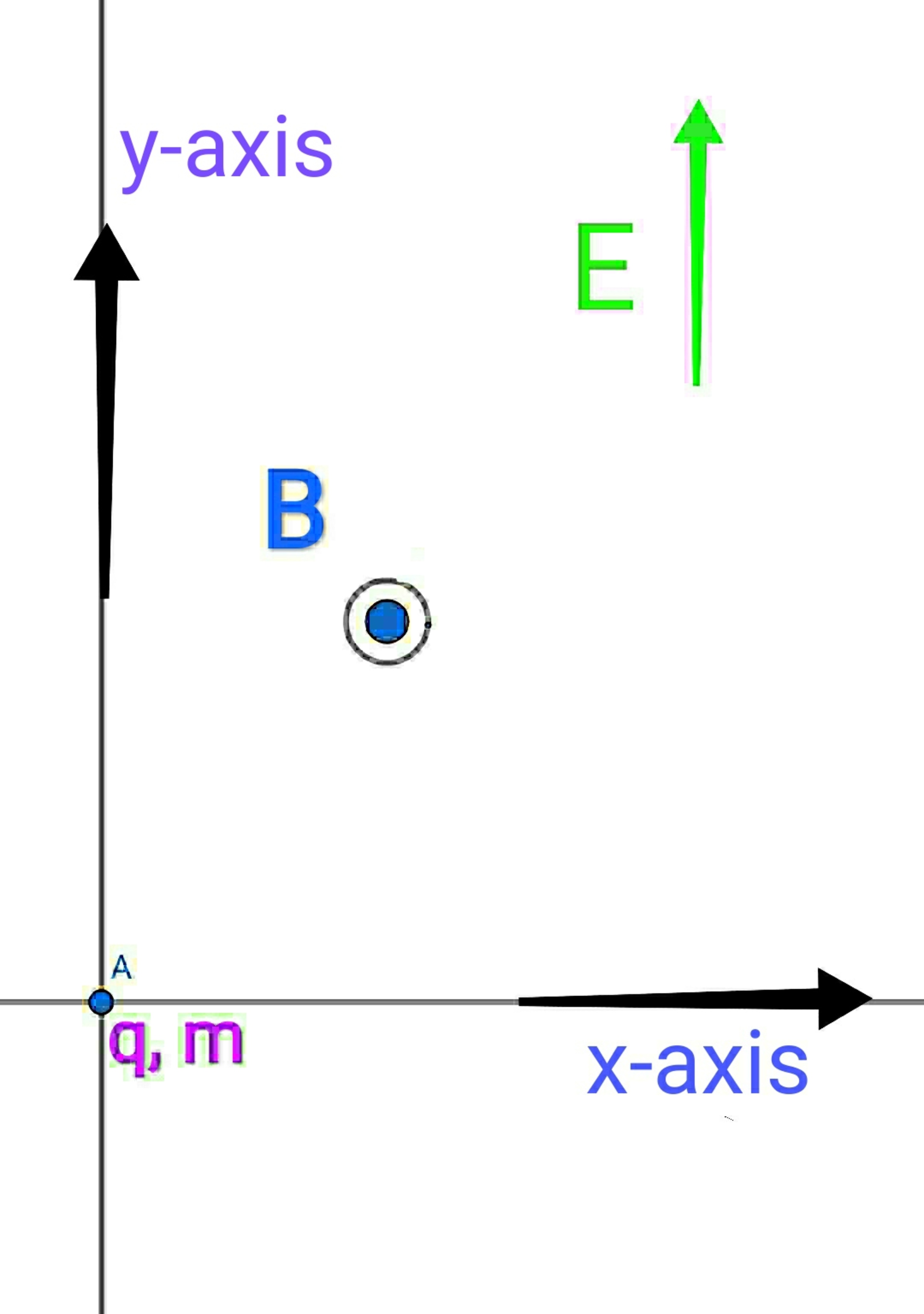 Find the
coordinate made by the particle over all time.
Find the
coordinate made by the particle over all time.
Details and Assumptions
1)
2)
3)
4)
5)
There is no gravity
The problem is not original
The answer is 0.64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
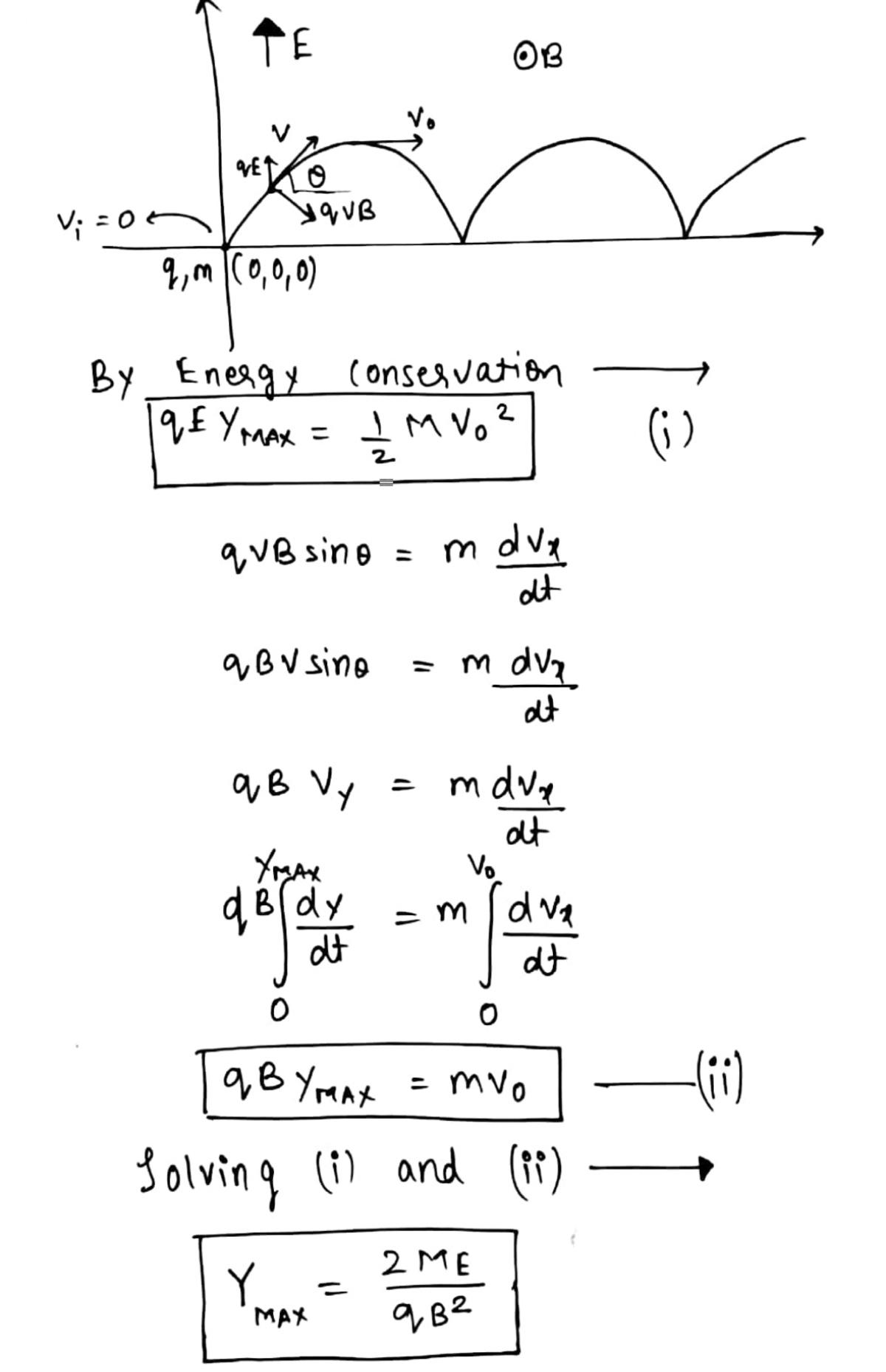
Force acting on the charge is
F = q ( E + v × B ) = q ( j ^ ( E − v x B ) + i ^ v y B ) .
So
d t d v x = m q B v y , d t d v y = m q E − m q B v x ⟹ d t 2 d 2 v y = − ( m q B ) 2 v y .
Solution of the last equation is
v y = A sin ( m q B t ) , where A, the amplitude of v y , is the integration constant. The other constant is zero since initial velocity is zero in both the x and the y directions. Since there is no acceleration in the z direction and the initial velocity in this direction is zero, there is no motion along this direction. So,
v x = q B m ( m q E − d t d v y ) = B E − A cos ( m q B t ) .
Since at t = 0 , v x = 0 ,
Therefore A = B E ⟹ v y = B E sin ( m q B t ) ⟹ y = q B 2 m E ( 1 − cos ( m q B t ) )
⟹ y m a x = q B 2 2 m E .
Substituting values, we get y m a x = 0 . 6 4