Electric Christmas Tree
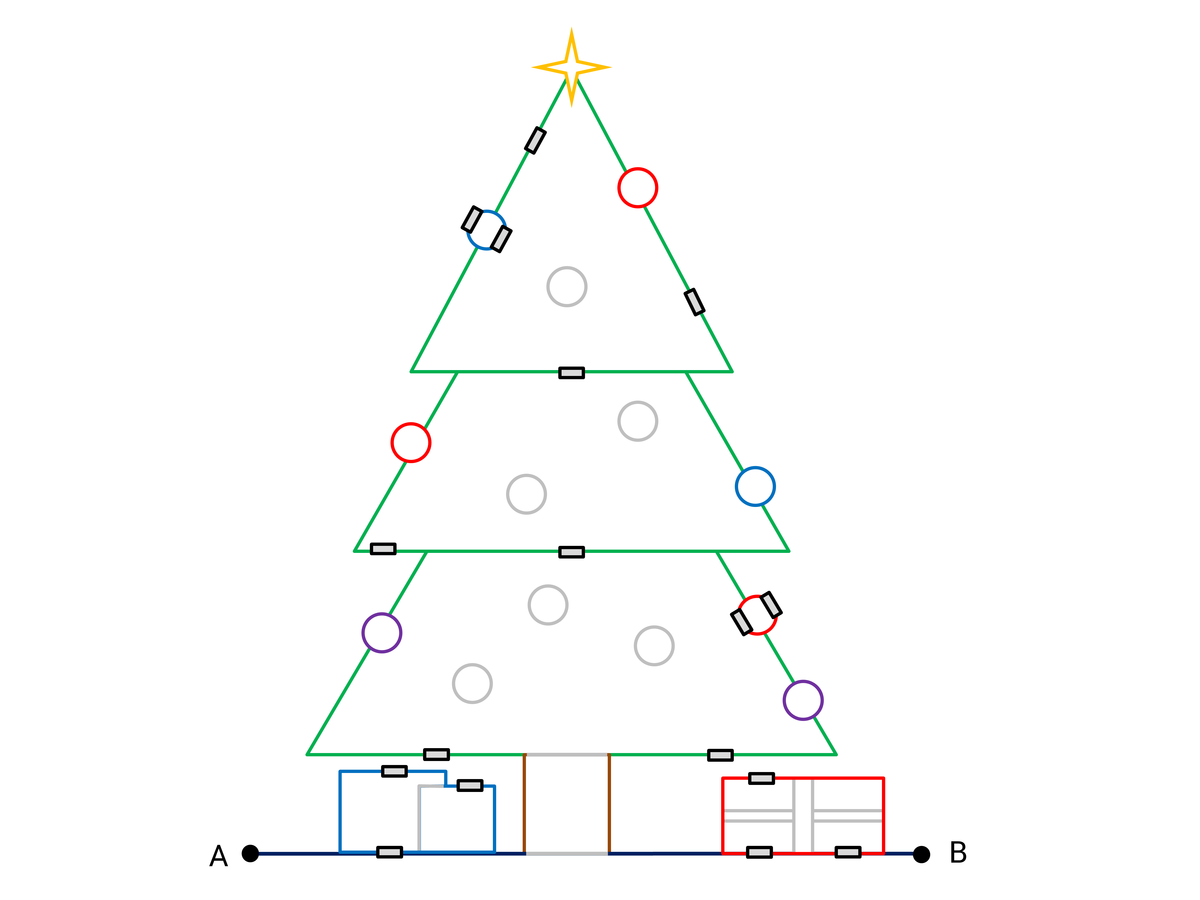
In the above circuit shaped like a Christmas tree, the 17 tiny grey rectangles are all resistors with identical resistance 1 ohm. (Light grey line segments are not part of the circuit.)
The effective resistance across A and B can be expressed as ohms, where and are coprime positive integers. Find . (Your answer should be three digits long)
Like this? See another related problem here .
The answer is 623.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The principles of Thevenin,s theorem can be applied in order to simplify the calculation for the total resistance across the entire circuit between A and B. By considering only a portion of the circuit at a time and then using the calculated equivalent resistance between selected points in subsequent calculations the circuit can be dealt with in manageable pieces.
The resulting total resistance can be calculated by applying these expressions
Resistors in Series R T o t a l = R 1 + R 2 + R 3 + . . .
Resistors in Parallel
R T o t a l = R 1 ∣ ∣ R 2 ∣ ∣ R 3 ∣ ∣ . . . Using || to indicate parallel resistances.
R T o t a l = R 1 + R 2 + . . . R 1 R 2 . . .
Beginning at the top of the diagram.
R 2 ∣ ∣ R 3 = R 2 + R 3 R 2 R 3 = 1 + 1 1 ∗ 1 = 2 1 Ω
R t o p = R R 2 ∣ ∣ R 3 + R 1 + R 4 = 2 1 + 1 + 1 = 2 5 Ω
Total equivalent resistance between points E and F considering only resistors. R1,R2,R3,R4,R5
R E F = R t o p ∣ ∣ R 5 = 2 5 + 1 2 5 = 2 7 2 5 = 7 5 Ω
R D G = ( R E F + R 6 ) ∣ ∣ R 7 = ( R E F + R 7 ) + R 7 ( R E F + R 7 ) ∗ R 7 = 5 / 7 + 1 + 1 5 / 7 + 1 = 1 9 / 7 1 2 / 7 = 1 9 1 2 Ω
R 1 2 + R 1 3 = 2 Ω
R U n d e r l e f t = ( R 1 2 + R 1 3 ) ∣ ∣ R 1 4 = 3 2 Ω
R U n d e r r i g h t = ( R 1 5 + R 1 6 ) ∣ ∣ R 1 7 = 3 2 Ω
R 8 ∣ ∣ R 9 = 2 1 Ω
R A B = R u n d e r l e f t + R 1 0 + R D G + R R 8 ∣ ∣ R 9 + R 1 1 + R u n d e r r i g h t = 3 2 + 1 + 1 9 1 2 + 2 1 + 1 + 3 2
L C D = 3 ∗ 1 9 ∗ 2 = 1 1 4
R A B = 1 1 4 7 6 + 1 1 4 1 1 4 + 1 1 4 7 2 + 1 1 4 5 7 + 1 1 4 1 1 4 + 1 1 4 2 7 6 = y x = 1 1 4 5 0 9 Ω
answer x+y = 509+114 = 623