Electric eels
An electric eel can generate a voltage of 6 0 0 V across its body. The eel does this via a system of up to 6000 “electroplaques” inside its body. What is the average strength of the electric field in V/m inside the body of a 1 0 cm wide eel?
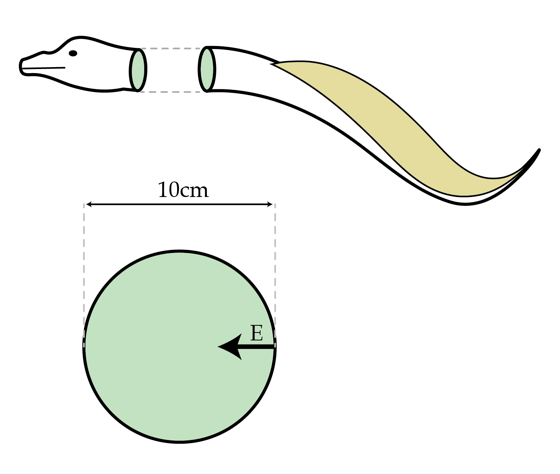
Details and assumptions
- Treat the opposite sides of the eel as the plates of a parallel plate capacitor.
The answer is 6000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
E = d V = ( 1 0 cm / 1 0 0 ) m 6 0 0 V = 0 . 1 m 6 0 0 V = 6 0 0 0 V/m
voltage of the eel is : 6 0 0 V
wide of the eel is : 1 0 c m or 0 . 1 m
E = q ( c h a r g e ) F ( E l e c t r i c F o r c e )
E = 0 . 1 m 6 0 0 V = 6 0 0 0 V / m
a little mistake , E = q F should be E = d i s t a n c e F ( E l e c t r i c F o r c e ) and Electric force is voltage.
In order to solve the problem we have to apply the theorem of gauss.
The flow σ is equal to σ = ∮ E δ ˙ S = 0 and to σ = ϵ 0 ∑ i = 1 n Q what we end up is a simple equation of E which is E = r V due to the fact that ϵ 0 = 4 π k 1 and that V = k r Q
Wow, by far the most advanced explanation for sure. Is it necessary to use such an analysis, rather than to simply assert that E = r V ?
There are 6000 Electroplaques, it means every 10 electroplaque produces 1 volt. Total length of eel is 10 cm, that means at every 1 cm there is an electroplaque, which can be treated as a parallel plate capacitor. Now, E = V/d = 600/(10 cm) = 600/(10x10^-2) = 6000
Given that the eel can generate at least 600 V in its body, I assumed that;
H=V/m
Where H is the variable for Electromagnetic Field. If what we are looking for is the strength of its electromagnetic field produce by its body we consider that the assumed equation is to followed.
Substituting the values with the given variables we get;
H= 600 V/ 10 cm
Since, the length is not in its standard form we need to convert it from centimeters to meter
10 cm x 1 m/ 100 cm = 0.10 m, thus
H= 600 V/ 0.10 m
H= 6000 V/m
V = E d ⇒ E = d V ⇒ E = 0 . 1 6 0 0 ⇒ E = 6 0 0 0