Electric Field at axis of Cylinder!
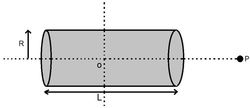 A non-conducting solid cylindrical rod of length
L
and radius
R
has uniformly distributed charge
Q
. Find the electric field at point
P
, a distance
L
from the center of the rod.
A non-conducting solid cylindrical rod of length
L
and radius
R
has uniformly distributed charge
Q
. Find the electric field at point
P
, a distance
L
from the center of the rod.
If E = a π R b L ϵ 0 Q [ L + ( d L c + R e ) f − ( i g L h + R j ) k ]
then, Find the sum of ( a + b + c + d + e + f + g + h + i + j + k ) .
Note : Fractions (ex 4 7 , 2 3 ) must not be simplified and written as 1 1 . 7 5 , 1 1 . 5
The answer is 30.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Nishant Rai The answer is not unique because 9/4 can be written in many different ways. 9/4 makes the most sense, which is why I got the answer, but still, it could be written as 2.25/1 or something.
Log in to reply
Yes......I agree with u coz my answer too was correct in its own sense
can you tell me how to find the electric field for a solid hemisphere on the axis of its base
Log in to reply
Consider rings and u will have to integrate this function KQ(x+rcosa)da/2(r²sin²a+x²)¾.² Its 3/2 X distance from axis Integrate for a=0 to a=π/2
Do u think its level 5 problem? Coz its just integration
Log in to reply
no its easy @Ace Pilot , u must proceed and it will be simplified ,
LOTS AND LOTS of integration, A difficult question for Std. XI student, We dont have Integration in std XI
We begin by considering the integral across all infinitesimal contributions to the overall electric field:
E = ∫ d E = ∫ ℓ 2 k d q = ∫ z 2 + r 2 k cos θ d q
Where θ is the angle that the radius extending from point P to some point in the cylinder makes with the horizontal, since the vertical components of force cancel each other out. We also know that d V = r d r d θ d x and d V d q = π R 2 L Q . This means that we will have:
E = π R 2 L k Q ∫ ∫ ∫ z 2 + r 2 cos θ r d r d θ d z
Since cos θ = ℓ z , we have:
E = π R 2 L k Q ∫ ∫ ∫ ( z 2 + r 2 ) 3 / 2 z r d r d θ d z ⇒ E ( P ) = R 2 L 2 k Q ∫ L / 2 3 L / 2 ∫ 0 R ( z 2 + r 2 ) 3 / 2 z r d r d z
Performing the u-substitution of u = r 2 and 2 d u = r d r , we get:
E ( P ) = R 2 L k Q ∫ L / 2 3 L / 2 ∫ 0 R 2 ( z 2 + u ) 3 / 2 z d u d z = R 2 L − 2 k Q ∫ L / 2 3 L / 2 [ z z 2 + u 1 ] ∣ ∣ ∣ ∣ 0 R 2 d z = R 2 L 2 k Q ∫ L / 2 3 L / 2 [ 1 − z z 2 + R 2 1 ] d z
Now, we perform another u-substitution, with u = z 2 and 2 d u = z d z , getting:
E ( P ) = R 2 L 2 k Q [ L − 2 1 ∫ L 2 / 4 9 L 2 / 4 u + R 2 1 ] d u = R 2 L 2 k Q [ L − 4 L 2 + R 2 + 4 9 L 2 + R 2 ] = 2 π R 2 L ϵ 0 Q [ L − 4 L 2 + R 2 + 4 9 L 2 + R 2 ]
Which leaves us with:
2 + 2 + 2 + 4 + 2 + 2 1 + 9 + 2 + 4 + 2 + 2 1 = 3 0
Consider a Disc of radius R of thickness d r at a distance r from the center O of the cylinder.
Charge on the disc,
d q = π R 2 L Q ( π R 2 d r ) = L Q d r
Electric field due to disc along it's axis
E x = 2 ϵ 0 σ [ 1 − x 2 + R 2 x ]
Do the necessary Integration and get the answer!
Final answer ⇒ E = 2 π R 2 L ϵ 0 Q [ L + ( 4 L 2 + R 2 ) 0 . 5 − ( 4 9 L 2 + R 2 ) 0 . 5 ]