Electric Field Due To Charge And Sphere
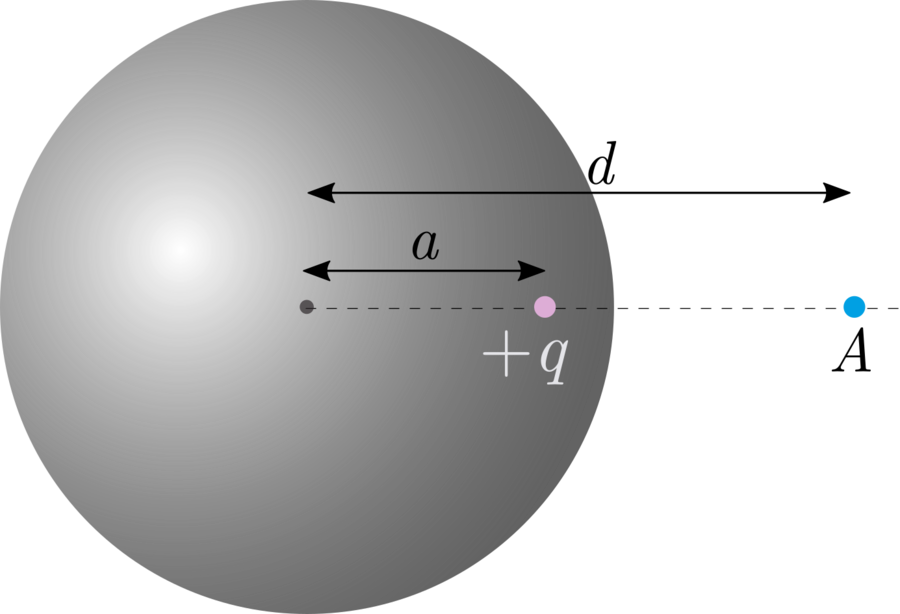
We have an uncharged, hollow, metal sphere of radius . We place a point charge in the sphere at a distance of from the center.
What is the magnitude of electric field at point outside the sphere, which is at distance from the center of the sphere?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the metal sphere had not been there, then the electric field at A would have been the electric field due to the point charge, + ( d − a ) 2 k q . However, when we place the metal sphere, the electrons in the sphere rearrange themselves, and as a result, the electric field at A changes.
Since the sphere is a conductor, electrons can move in it freely. When the electrons in the sphere attain equilibrium, they are not moving anymore, which means that the potential is constant throughout the volume of the conductor. This implies that the electric field inside the volume of the conductor.
We can use Gauss' law to show that charge − q is induced on the inner surface of the sphere, and charge + q is induced on the outer surface of the sphere. Consider a sphere, (shown in yellow dashed line) as the Gaussian surface. The surface of the sphere is in the conductor, so the electric field at every point of the sphere's surface is zero. By Gauss' law,
∫ E ⋅ d A = ϵ 0 Q
the net charge enclosed within the Gaussian surface is zero. There is a point charge + q inside the Gaussian surface, so there must be − q charge induced on the inner surface of the sphere.
Since the net charge on the sphere is zero, a charge + q is uniformly induced on its outer surface.
The net electric field due to the inner surface of the sphere and the point charge cancel each other out. What remains is the electric field due to the charge on the outer surface of the sphere. Its electric field is identical to the electric field of a point charge + q placed at the center of the sphere. Hence, the net electric field at point A is given by + d 2 k q 2 .