Electric Field Locus
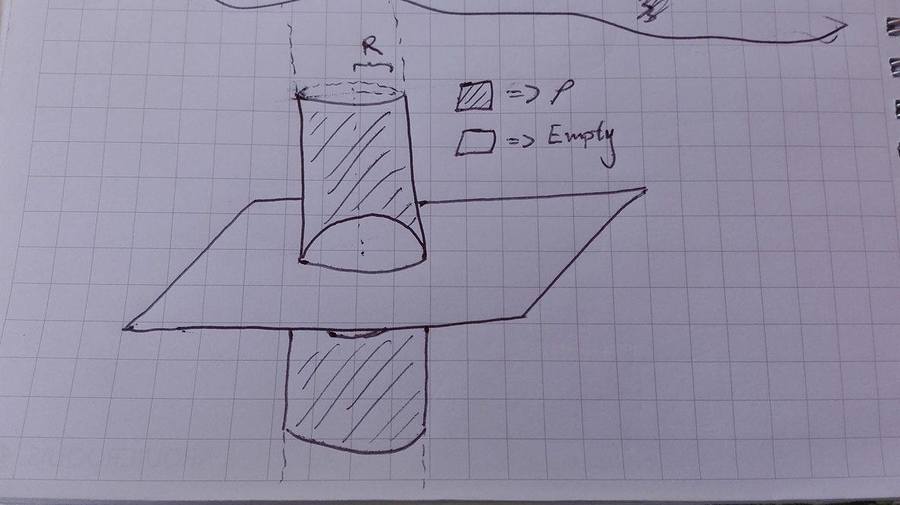
A solid infinite cylinder of equation has a uniform charge density . It also has a spherical cavity which is represented by the equation . The locus, in the plane, where the electric field is maximum is a circle of radius , where and are coprime positive integers.
Find the value of .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At first we'll denote the Cillynder-Sphere system as the superposition of the whole cillynder ( c ) with charge density ρ and a sphere ( s ) with charge density − ρ . So, for using Gauss's Law we have: ∮ E c ⋅ d A = ϵ 0 Q e n c l o s e d ⇒ E c ( r ) = 2 ϵ 0 r R 2 ρ r ^ ∮ E s ⋅ d A = ϵ 0 Q e n c l o s e d ⇒ E s ( r ) = − 3 ϵ 0 r 2 R 3 ρ r ^ ⇒ E ( r ) = ϵ 0 R 2 ρ ( 2 r 1 − 3 r 2 R ) ⇒ max E ( r ) = E ( 3 4 R ) = 1 6 ϵ 0 3 R ρ All of this is for r ≥ R , but it's easy to find out that, by the same way, the electric field for r < R gets: E ( r ) = 6 ϵ 0 r ρ ⇒ max ( E ( r ) ) = E ( R ) = 6 ϵ 0 R ρ < 1 6 ϵ 0 3 R ρ So the locus on the whole plane in which the electric field is maximum is a circle with center at the origin and radius 3 4 R