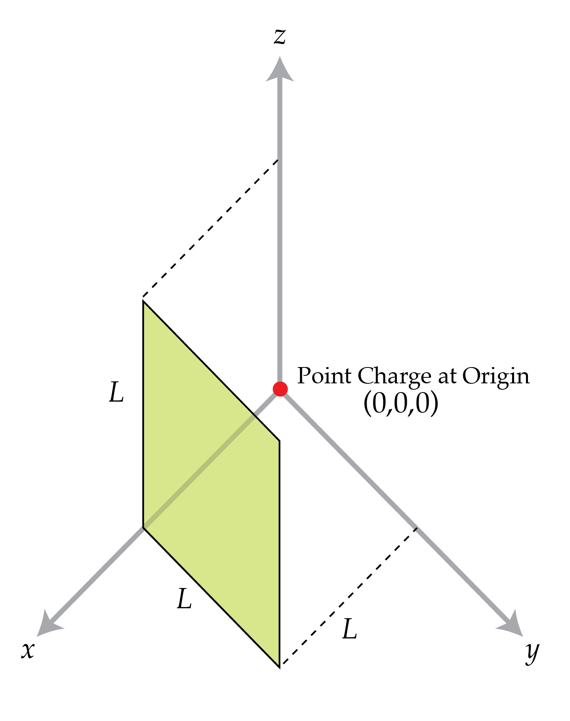
Electric flux through a square.

Imagine that $q$ is at the center of a cube with side length $2L$ . By Gauss's Law, the flux through the cube is $\Phi_E = \frac{q}{\epsilon_0}.$ The flux through one face of the cube is, by symmetry, $\frac{\Phi_E}{6}=\frac{q}{6\epsilon_0}.$ The flux through a quarter of a face (the square with which we are concerned) is, by symmetry, $\frac{\Phi_E}{24}=\frac{q}{24\epsilon_0}$ $=\frac{10^{-9} \ \mathrm{C}}{24\left(8.85 \times 10^{-12} \mathrm{\frac{F}{m}}\right)} =\fbox{4.71 V·m}.$

Gauss's law states that the flux through any closed surface is equal to $\frac{Q}{ϵ_0}$ , where $Q$ is the total charge inside the surface and $ϵ_0$ is the permittivity of free space. Consider the cube of length $2L$ centered around the origin. Imagine this is a 2x2 Rubik's Cube! the square of length $L$ in the problem is analogous to a sticker on one face of the cube. By symmetry, the flux through each "sticker" will be the same. Since there are 24 of these "stickers" on the surface, the flux through one "sticker" is: $Flux = \frac{Total Flux}{24} = \frac{Q}{24ϵ_0} = \frac{1nC}{24ϵ_0} = 4.71 V \cdot m$

Utilizing this symmetry and dividing each cube face into four LxL areas to meet the requirement of the question, we have 6x4=24 LxL sized areas around the centered charge through each equal flux passes due to symmetry. So the computation gives: Flux through LxL area=1nC/(ϵ0 16)=E-9/(16 8.85E-12)=4.708

Construct a cube of side length $2L$ around the charge $q$ , with the charge in the centre. Divide the surface of the cube into 24 congruent squares of side length $L$ by partitioning each face of the cube into four quarters. One of these squares is the square that we are interested in. Due to symmetry (by rotation or flipping about the charge, each square can be made to occupy the position of each of the other squares), the electric flux through each square is the same.

Since the cube completely encloses the charge, by Gauss's law, the total electric flux through the cube is $\phi_{E}=\frac{q}{\epsilon_0}$ . Thus the electric flux through each square is $\frac{1}{24} \times \frac{q}{\epsilon_0} \approx 4.708 \, V \cdot m$

Consider a cube of side length 2L that is centered at the origin. By Gauss' Law, the electric flux through this cube is

$Φ_{cube} = q/ε_{0}$

Because each face of the cube has 4 of the desired figure, and there are 6 faces, we simply take the flux from above and divide by 24. We can do this because if we split up each face of the cube into 4 identical squares, they are all identical to each other. Therefore, the flux through the smaller square is

$Φ_{smaller square} = Φ_{cube} /24 = q/24*ε_{0}= 4.708$

Let's imagine a cube with each side measuring $2L$ , with the charge at it's center. By Gauss's Theorem, the electric flux through the cube's surface is

$\Phi(\vec{E})$ $)= \frac{q}{\epsilon_{0}}$

If we divide each face of the cube in 4 squares, equal to the original one, we notice the situation is totaly symmetrical.

So if we divide the total flux by $24$ we obtain the electric flux through the original square, which is $4.7 \: V \cdot m$

From Gauss' law we know the total electric flux ( X ) through a closed Gaussian Surface X = $\frac{Charge Enclosed}{Epsilon 0}$ . Now we must find an appropriate Gaussian Surface with an ideal symmetry. By inspection we imagine surrounding the point charge with a Cube where the point charge is the centre and our flat square is at the top left quarter of one side of the cube. By symmetry the electric flux through each side is the same and through each quarter of each side. As we can define 24 ( $4 \times 6$ ) such surfaces on our cube all with the same flux through them which add to give the total flux, our required flux is $\frac{X}{24}$ = (Roughly) 4.708 .

Our main aim is to convert this question/diagram in such a way that Gauss's Law can be easily applied. For that, first assume a cube of length 'L" around the charge(this cube also includes the side which the question speaks of). The charge now, is located on one of the vertices of the cube.

Now, add another cube of same length (L) along the Y,Z and -ve X axis.We have got a cuboid with the charge at the vertex of the same. Now add another CUBOID of the same dimensions about Z,X and -ve Y axes. The charge now, is located on the edge length of the bigger/newer cuboid. Add another IDENTICAL cuboid on top of this cuboid. We have successfully positioned the charge in the exact centre of the new cube.

Using Gauss' Law--> Flux = Charge enclosed/Eo. For a single cube--> Phi= q/8Eo (since 8 cubes are involved) and for a single face of one cube, Phi=Q/24Eo (Since charge present on the vertex of a cube creates flux only on three sides.) Substitute the value for Q/24Eo and you will get your answer!