Electric Mushroom !
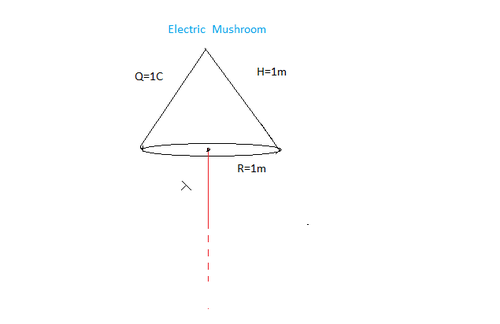 Let a solid uniformly charged cone having total charge
Q
, radius
R
and height
H
is kept in contact with uniformly charged wire having charge per unit length
λ
as shown. Then calculate the electric interaction force between them and report your answer to nearest integer.
Let a solid uniformly charged cone having total charge
Q
, radius
R
and height
H
is kept in contact with uniformly charged wire having charge per unit length
λ
as shown. Then calculate the electric interaction force between them and report your answer to nearest integer.
Details and Assumptions
Q R H λ 4 π ϵ 1 = = = = = 1 C 1 m 1 m 1 0 − 9 C m − 1 9 × 1 0 9 N m C − 2
Try more Deepanshu's Mixing of concepts
This is Original.
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
did just like you ! :)
Hey that should be force per unit length.for calculating the force we need atleast 2 magnitude of charges if lambda is given so must the length be.
 Amazing problem, refreshed a lot of my concepts in one go!
Amazing problem, refreshed a lot of my concepts in one go!
Except i did it by using the electric field of a wire instead of the cones,
the electric field paralell to the wire of a semi infinite wire is given by
h k λ s i n ( θ )
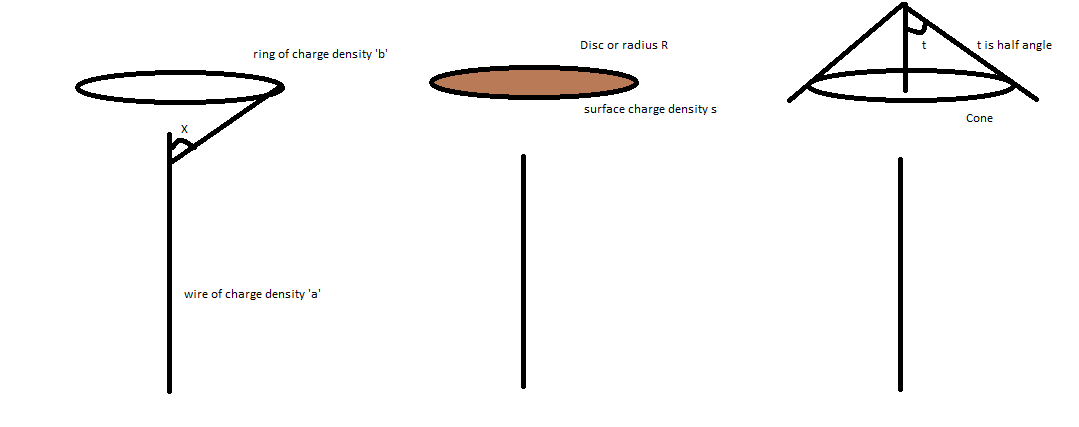
where λ is the charge density and h is the distance from the axes, and θ is the angle shown in figure as x
if we are dealing with a ring of radius R concentric with the axis of the wire, then h = R
so the electric force on a ring of radius R is
E × 2 π R × λ 2
2 ϵ λ λ 2 s i n ( θ )
where λ 2 is the linear charge density of ring
If the ring is actually a small part of a disc whose surface charge density is σ , Then since λ 2 = σ d r then the force of interaction is given by
2 ϵ σ λ [ s i n ( θ ) ] d r ]
Now we are ready to deal with the c o n e
Now to make things treatable, let us right sin ( θ ) interms of distance of the disc from the tip of wire,
using the fact that s i n ( θ ) = R 2 + z 2 R
we rewrite the previous expression for a fixed z as
∫ 0 R ( 2 ϵ σ λ R 2 + z 2 R ) d r = 2 ϵ σ λ ( R 2 + z 2 − z )
Now we are ready,
finally, the surface charge density of the thin disc is related to that of the cone by the formula
ρ d z = σ
also R which is the radius of the thin disc can be written in terms of z as
R = t a n ( α ) ( H − z ) where ' α ' is the half angle
so substituting this and putting proper limits, we get the integral (H is the height of cone)
∫ 0 H 2 ε λ ρ [ ( H − z ) 2 t a n ( α ) 2 + z 2 − z ]
Now putting H=1 and tan ( α ) =1
and also that ρ = 3 π R 2 H Q
W e g e t t h e a n s w e r a s 1 6 . 7 9 4
since nearest integer is asked, Final answer is ⌈ 1 6 . 7 9 4 ⌉ = 1 7
Thanks for taking Time for writing Solution !
Log in to reply
Hey, i have learnt latex and now have updated all symbols in answer as you can see, but can you tell how to avoid using /quad again and again in texts
Nice Problem, Loved working on it.
From the image I belive it is clear how I have taken elements and what are my variables.
Now I am using a result,that electric field on a point on the axis at a distance z due to a charged disk having radius a and charge q is given by :
E = 2 π ε 0 a 2 q ( 1 − z 2 + a 2 z )
Now force on a elemental charged length d x of wire due elemental charge on the disk element is given by :
d 2 F = 2 π ε 0 ( R ( 1 − y ) ) 2 λ H 2 d x d q ( 1 − ( x + y ) 2 + ( H ( 1 − y ) R ) 2 x + y )
Now d q = π ρ d y ( H R ( 1 − y ) ) 2
Putting this we have :
d 2 F = 2 ε 0 λ ρ ( 1 − ( x + y ) 2 + ( H ( 1 − y ) R ) 2 x + y ) d x d y
Finally we get the expression of F as :
F = 2 ε 0 λ ρ ∫ 0 H ∫ 0 ∞ ( 1 − ( x + y ) 2 + ( H ( 1 − y ) R ) 2 x + y ) d x d y
Putting the value of ρ we get :
F = 2 π ε 0 R 2 H 3 λ Q ∫ 0 H ∫ 0 ∞ ( 1 − ( x + y ) 2 + ( H ( 1 − y ) R ) 2 x + y ) d x d y
Putting all the values and simplifying we get :
F = 5 4 ∫ 0 1 ∫ 0 ∞ ( 1 − ( x + y ) 2 + ( 1 − y ) 2 x + y ) d x d y
F = 2 2 7 l n ( 1 + 2 ) = 1 6 . 8 2 N
Since you asked to round to the nearest integer hence the answer is 1 7