Electric potential due to conductors and cavities

Electricity and Magnetism Level 2

Inside a neutral spherical conductor, a spherical cavity is present. A charge Q is placed inside the cavity. What is the electric potential at the center (C) of the cavity?

In the diagram above,

$r_1$ is the distance of the charge from the cavity's center C;
$r_2$ is the radius of the cavity;
$r_3$ is the distance between the centers of the sphere and cavity;
$r_4$ is the radius of the sphere.

\frac{{kQ}}{{{r_1}}} - \frac{{kQ}}{{{r_2}}} + \frac{{kQ}}{{{r_4}}}

\frac{{kQ}}{{{r_1}}} + \frac{{kQ}}{{{r_2}}} + \frac{{kQ}}{{{r_4}}}

\frac{{kQ}}{{{r_1}}} - \frac{{kQ}}{{{r_2}}} - \frac{{kQ}}{{{r_3}}} + \frac{{kQ}}{{{r_4}}}

\frac{{kQ}}{{{r_1}}} + \frac{{kQ}}{{{r_2}}} + \frac{{kQ}}{{{r_3}}} + \frac{{kQ}}{{{r_4}}}

1 solution

R G Staff
Jan 3, 2017

There will be three charge distributions, one is the charge Q itself and the other two will be due to induction on the surface of the cavity and the outer surface of the sphere.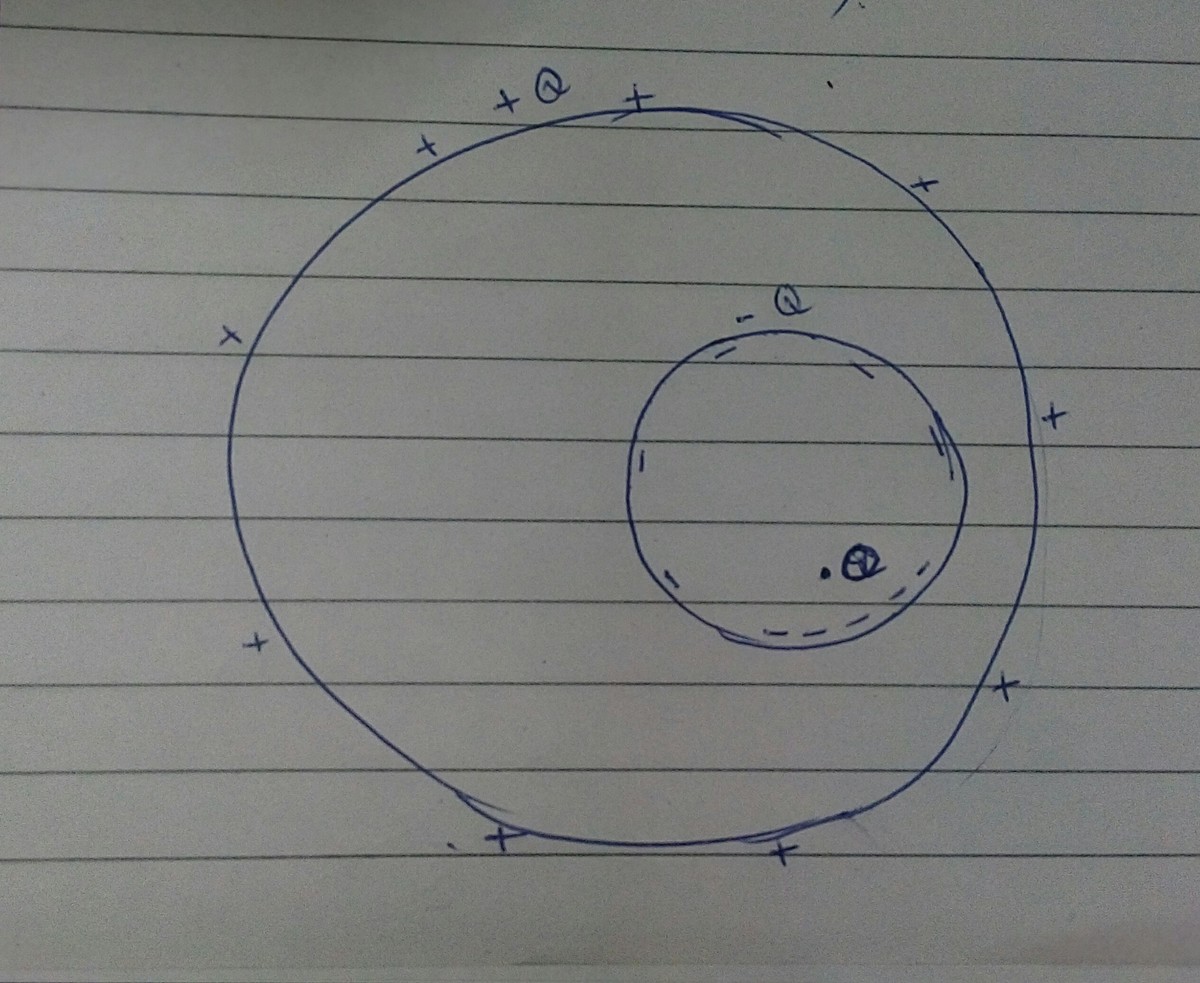

On the surface of the cavity -Q charge will be induced and on the outer surface of the sphere, an equal charge +Q will appear to keep the conductor neutral. The charge induced on the surface of the cavity will be non-uniform, its density near the point charge -Q will be greater. However, the whole charge on the cavity is at a distance $r_2$ from the center C.
The charge appearing on the outer surface will be uniformly distributed due to the shielding effect of the cavity.
Therefore, the net potential at the center C can be calculated by the adding the potentials due to the charge Q and the induced charges.
Therefore,
$V_C=\frac{{kQ}}{{{r_1}}} - \frac{{kQ}}{{{r_2}}} + \frac{{kQ}}{{{r_4}}}$

Electric potential due to conductors and cavities

1 solution

0 pending reports