Wonders Electrical Engineers Do With Bulbs!
You sneak into the house of a famous Electical Engineer in your town.
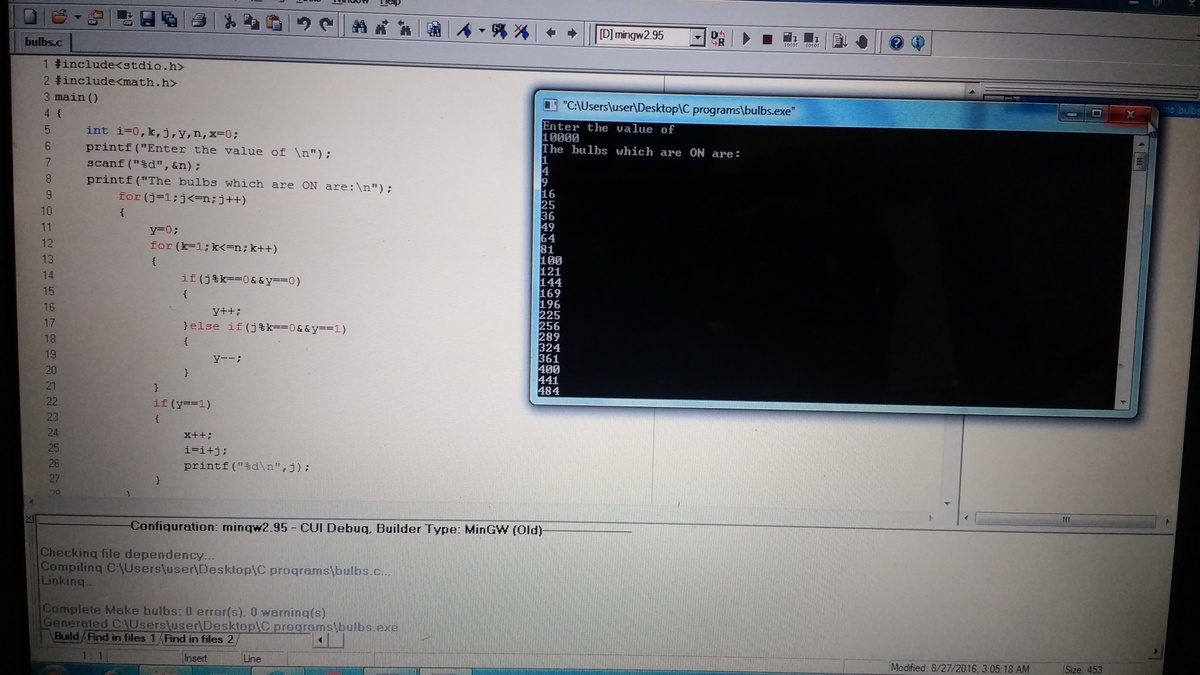
You find a weird arrangement of 10000 bulbs and 10000 switches (which are numbered in ascending order) in front of you. You see the main power button to this and out of curiosity you press it and suddenly the door behind you gets locked and the bulbs start glowing and the switches start toggling on/off in a weird pattern.
After some time the glowing stops.In front of the arrangement a board reads as follows:
- During the first pulse all the switches (with corresponding numbers) that are divisible by 1 are switched on.
- During the second pulse all the numbers that are divisible by 2 toggle (change to on if it's off, or change to off if it's on).
- During the third pulse all the numbers that are divisible by 3 are made to toggle and so on until 10000 pulses.
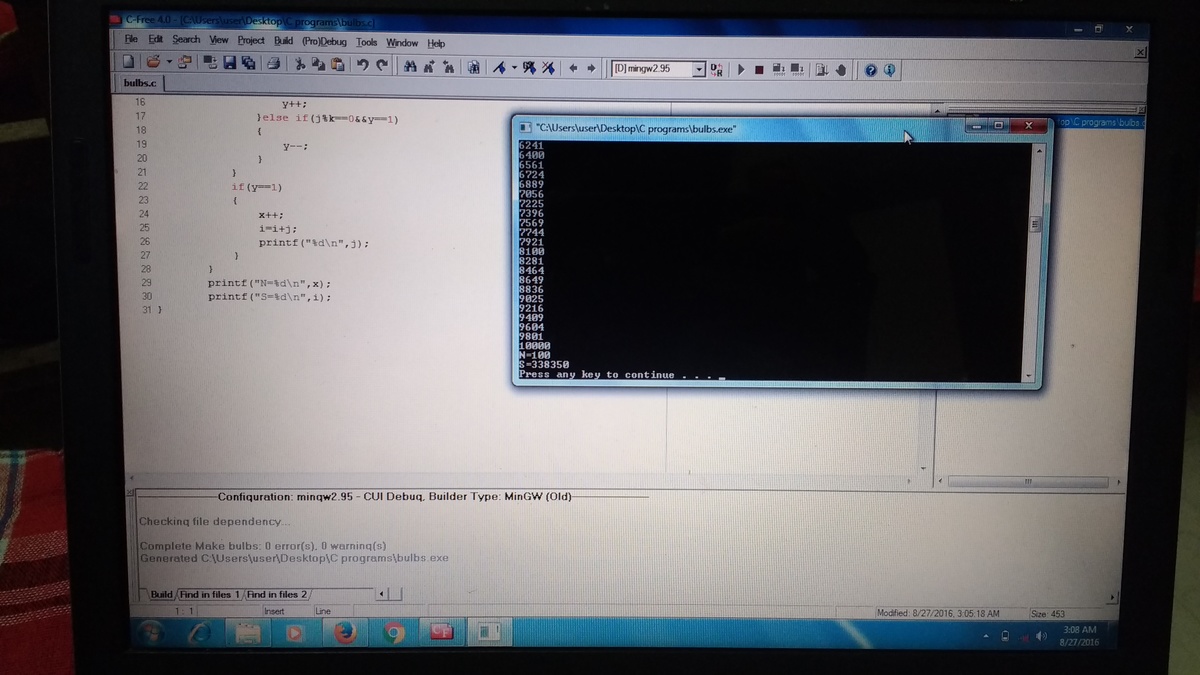
- At the end of pulse let denote the number of bulbs that are glowing and let denote the sum of the corresponding numbers of the bulbs that are glowing.
- Enter the answer as to open the door.
The answer is 338450.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Behold the power of a pure functional programming language!
The time complexity of this solution is Θ ( n )
Proof of how only squares work:
Let τ ( n ) denote the number of positive divisors of n (including both 1 and n ).
Before the first pulse, all the bulbs are off (call this the 0 state and call the on state as the 1 state). After the all of the 10000 pulses, say the i t h bulb is in state r . Then we claim that r ≡ τ ( n ) ( m o d 2 ) . The proof of this easy to see if the toggling function (T) is seen as follows : T : { 0 , 1 } → { 0 , 1 } T ( i ) ≡ i + 1 ( m o d 2 )
Hence the i t h bulb is on if and only if τ ( i ) is odd.
We show now that τ ( i ) is odd if and only if n is a perfect square.
Let n = i ∏ p i α i where p i is a prime for all i .
Then it follows that if d ∣ n then d = i ∏ p i β i 0 ≤ β i ≤ α i
Hence, τ ( n ) = i ∏ ( 1 + α i ) The desired conclusion now follows.