Electrified
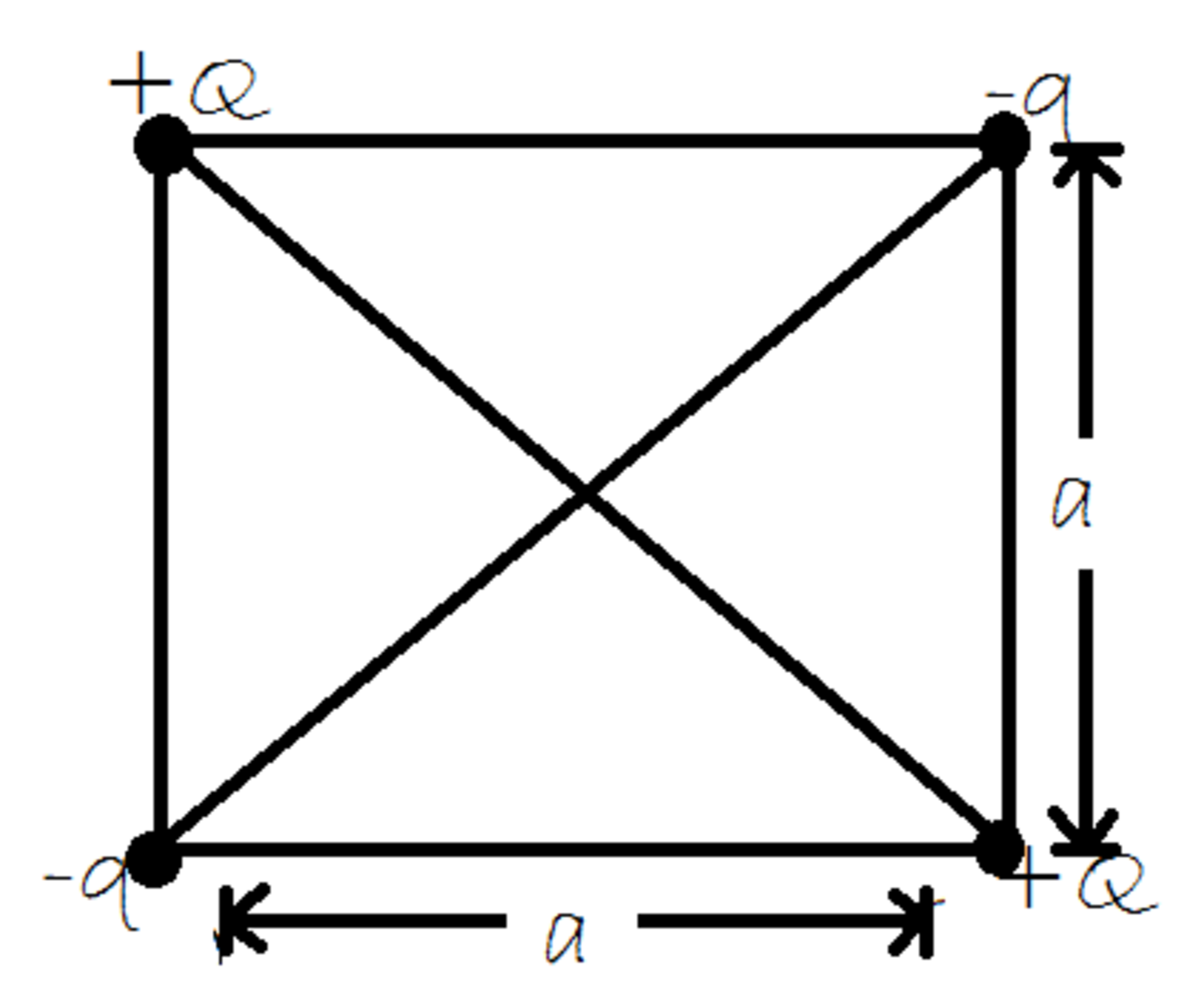
The charges with magnitude are held fixed in place by external unspecified forces. The charges with magnitude are free to move.
If the system is in equilibrium, find to 2 decimal places.
The answer is 2.82.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Such a system where all of the four charges are in equilibrium is impossible. Invesitgating the forces on either of the Q + yields the ratio: q Q = 2 2 . But, while equilibrating the forces on either q − charge rapidly yields: q Q = 2 2 1 which is contradictory with what we found before. This is due to the fact that any charge feels the same force along the square side, directly towards the charge on the adjacent vertex but if Q = q the force that the charges feel in the diagonal direction, directly away from the charge from the opposite vertex will never be same, hence is impossible to balance the system. If those forces were meant to be the same would meant that all the charges should have the same magnitude and, consequently, the forces that they would feel to the sides would be greater than thhose in the diagonal direction and, again, the forces won't balance. P.D. I entered my solution as: q Q = 2 2