Electro-Mechanics with Source
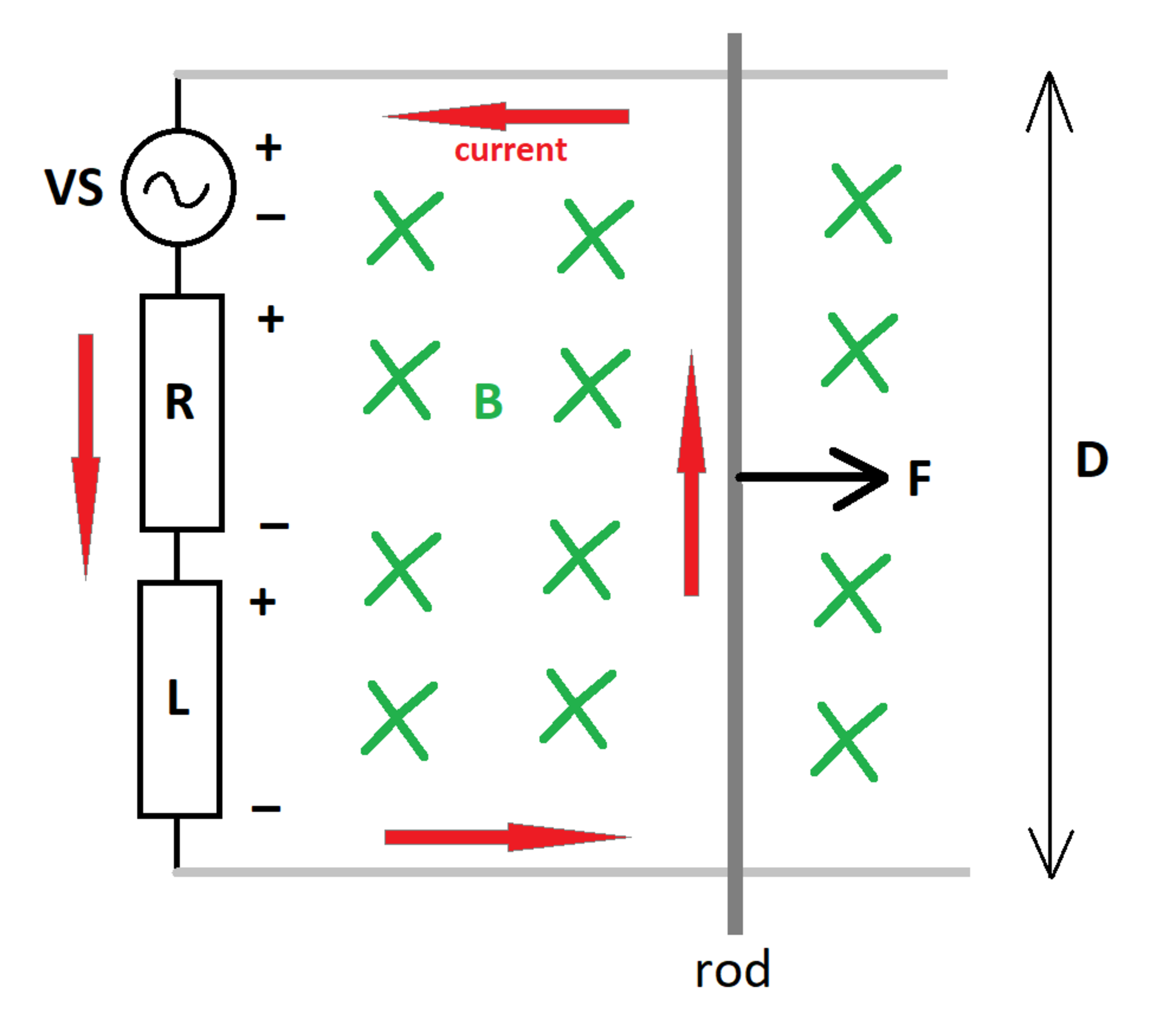
A conducting rod of mass slides along a pair of conducting rails which are separated by a distance . The rod is pulled rightward by a constant force . The circuit is completed by a series combination of a resistor , an inductor , and an AC voltage source . There is an ambient magnetic flux density which points into the page.
At time , the rod has zero speed and there is no current in the circuit. At time , how far is the rod from its initial position?
Details and Assumptions:
1)
2)
3)
4)
5)
6)
7)
8)
There is no gravity
9)
Neglect the magnetic field contributions from the rails
The answer is 0.1643.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
F u n P r o b l e m
As always, it is a pleasure to solve your problems. Thank you for another good one.
The basic equations are B v D − 1 0 s i n ( 5 t ) − i R − L d t d i = 0 F − B i D = m d t d v After substituting value 1 0 v − 1 0 s i n ( 5 t ) − 2 i − i ˙ = 0 v ˙ + 1 0 i = 2 Solving both equations, gives the differential equation in terms of v 1 0 v + 0 . 2 v ˙ + 0 . 1 v ¨ = 1 0 s i n ( 5 t ) + 0 . 4 Solving this differential equation and using initial conditions v ( 0 ) = 0 v ˙ ( 0 ) = 2 to find the values of arbitrary constant in the solution of differential equation. And after substituting the value of arbitary constants gives the solution of differential equation as v = 1 . 3 1 0 0 4 s i n ( 5 t ) − 0 . 4 3 9 7 5 7 3 0 3 e − t s i n ( 9 . 9 4 9 8 7 t ) + 0 . 1 7 4 6 7 2 e − t c o s ( 9 . 9 4 9 8 7 t ) − 0 . 1 7 4 6 7 2 c o s ( 5 t ) + 0 . 0 4 Substituting v = d t d x d t d x = 1 . 3 1 0 0 4 s i n ( 5 t ) − 0 . 4 3 9 7 5 7 3 0 3 e − t s i n ( 9 . 9 4 9 8 7 t ) + 0 . 1 7 4 6 7 2 e − t c o s ( 9 . 9 4 9 8 7 t ) − 0 . 1 7 4 6 7 2 c o s ( 5 t ) + 0 . 0 4 ∫ x ( 0 ) x ( 5 ) d x = ∫ t = 0 t = 5 ( 1 . 3 1 0 0 4 s i n ( 5 t ) − 0 . 4 3 9 7 5 7 3 0 3 e − t s i n ( 9 . 9 4 9 8 7 t ) + 0 . 1 7 4 6 7 2 e − t c o s ( 9 . 9 4 9 8 7 t ) − 0 . 1 7 4 6 7 2 c o s ( 5 t ) + 0 . 0 4 ) d t x ( 5 ) = 0 . 1 6 5 0 8 7