Electro-mechanics
This problem is based on a suggestion from Neeraj Anand Badgujar
A conducting rod of mass slides along a pair of conducting rails which are separated by a distance . The rod is pulled rightward by a constant force . A series combination of a resistor and an inductor completes the circuit. There is an ambient magnetic flux density which points into the page.
Initially, the rod has zero speed and there is no current in the circuit. As the elapsed time approaches infinity, what is the rod's steady-state speed?
Details and Assumptions:
1)
2)
3)
4)
5)
6)
7)
There is no gravity
8)
Neglect the magnetic field contributions from the rails
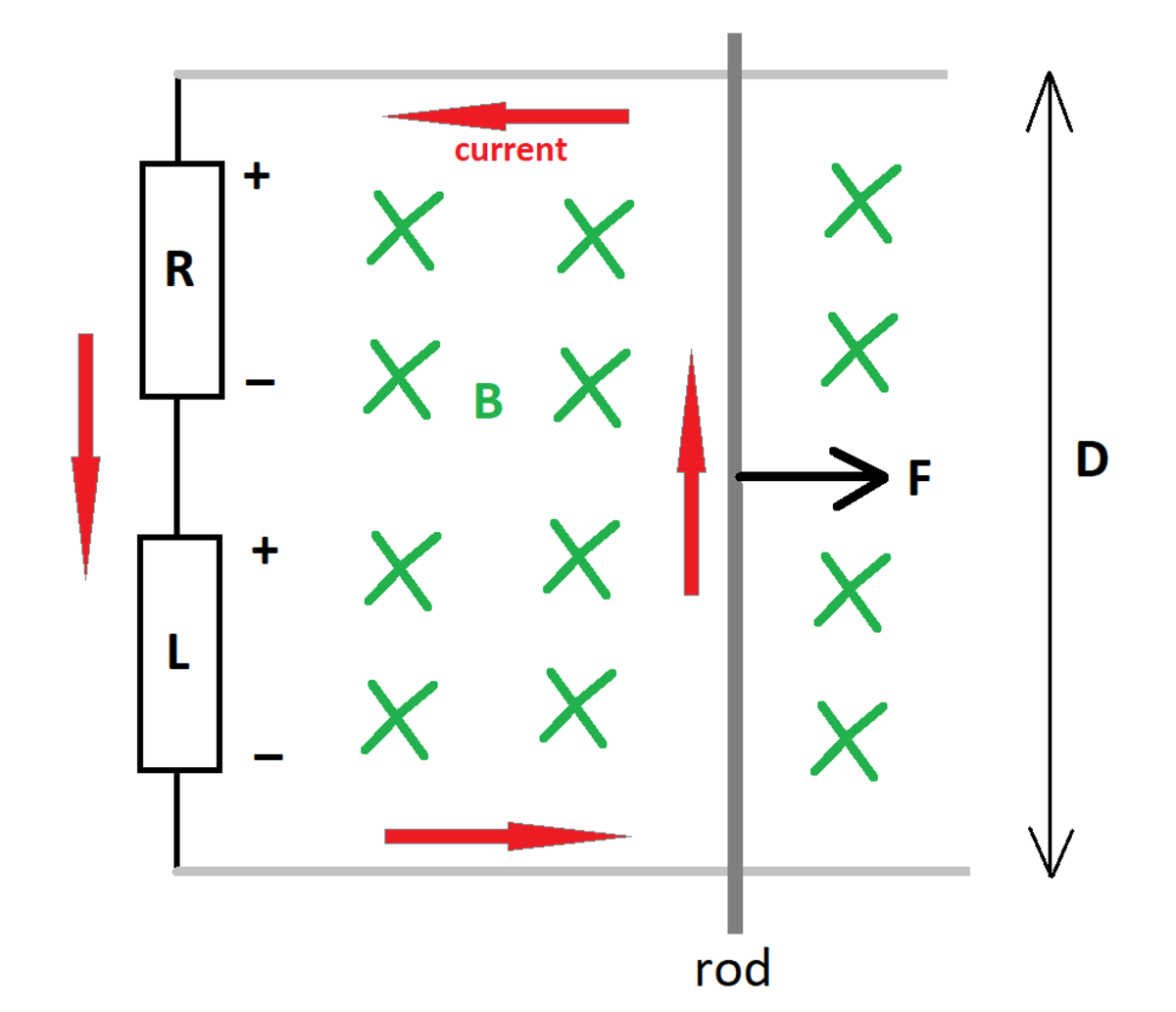
The answer is 0.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
F u n P r o b l e m
I was struggling in this question from last 1hr because I was taken D = 1 instead of 2 . So it's a lesson for me to read the data carefully.
Now come to the question. The basic equations are B v D − i R − L d t d i = 0 F − B i D = m a After substituting correct value you will reach 1 0 − 1 0 i = v ˙ 1 0 v − i = i ˙
In steady state velocity is constant, Therefore v ˙ = 0 and i ˙ = 0
Now ,by solving equations you will reach v s t e a d y = 0 . 1
Edited : I have 2 more methods .
2 nd method : At steady state v = c o n s t a n t a = 0
Net force in rod is zero.
Let current be I (which is constant at steady state) I = R B D v
Magnetic force on rod F m = B I D = R B 2 D 2 v
At Equilibrium F e x t = F m R B 2 D 2 v = F v = B 2 D 2 F R v s t e a d y = 0 . 1 (3) rd method:
Workdone by Force F = Heat dissipated in resistor R
As d T d I = 0 . Hence inductor offers 0 resitance and hence energy stored in it becomes constant.
At this moment . Let the velocity of rod is v
Power dissipated in resistor R I 2 R = R B 2 D 2 v 2 . R B 2 D 2 v 2 = F v cos 0 ° v s t e a d y = 0 . 1
I hope you enjoyed all these 3 methods.