Electrochemistry+Capacitors+Current Electricity
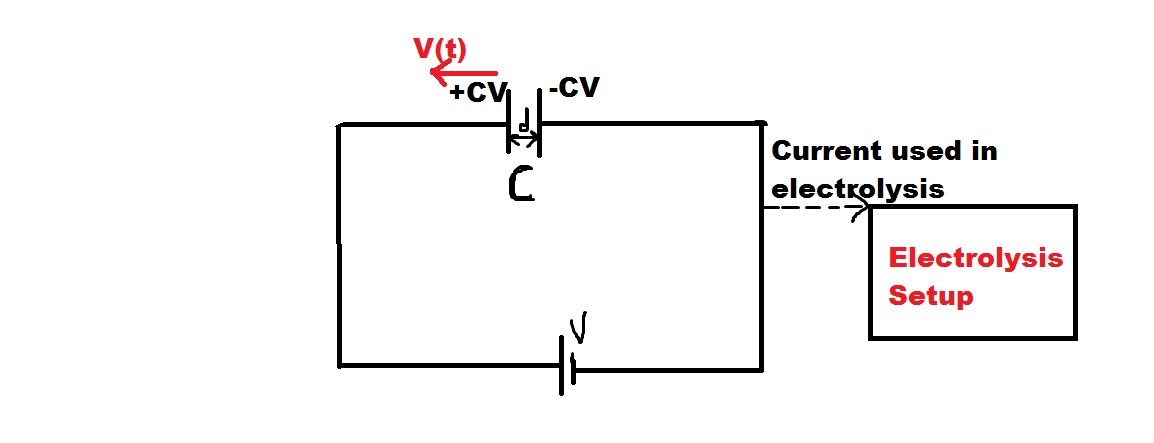
The given picture shows a system. The capacitor is initially charged till steady state and contains a dielectric of dielectric constant . The battery is connected in the whole experiment throught .
Our Aim with this setup is to use the magnitude of current developed in the circuit for electrolysis of and check what is the mass deposited on the cathode after a certain time from the beginning.
Initially, the capacitor plates are at a distance of . One of the plates is fixed and the other plate can be moved(after charging).
We start to move one of the plates with time-varying velocity .
The mass of Silver deposited in the time s to s be grams.
Input the value of
Details and Assumptions
-
a = 1
-
b = 2
-
d = 4
-
K = 10
-
t= 2 secs
-
Area of each plate = 100 .
-
is permeability of free space.
-
[The EMF of the battery]
-
Take Faraday's Constant as
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Fundamental capacitor equation:
Q = C V
Rate of change of charge:
Q ˙ = C V ˙ + V C ˙ = V C ˙
Capacitance formula:
C = d K ϵ 0 A C ˙ = − d 2 K ϵ 0 A d ˙
Plugging into charge rate of change:
Q ˙ = − d 2 V K ϵ 0 A d ˙ d ˙ = 2 a t + b
Total charge transfered (only magnitude matters):
Δ Q = ∫ 0 2 d 2 V K ϵ 0 A d ˙ d t = V K ϵ 0 A ∫ 0 2 d 2 d ˙ d t
We get one mole of silver for every mole of electrons. The number of moles of silver at the cathode is therefore:
N = F Δ Q
There are approximately 1 0 8 grams for each mole of silver. The total mass, in grams, is therefore:
M t o t = 1 0 8 F Δ Q = F 1 0 8 V K ϵ 0 A ∫ 0 2 d 2 d ˙ d t
Evaluating the integral numerically and plugging in numbers yields a total mass of 1 8 ϵ 0 grams.