ElectroMechanics and Capacitor

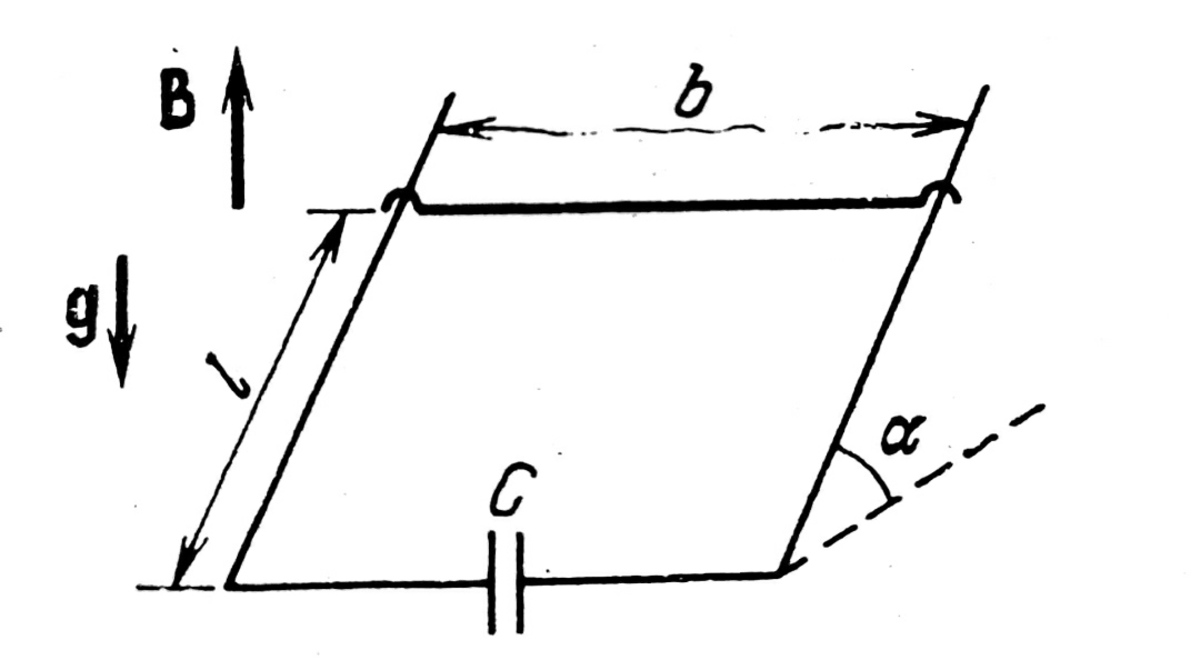
A metal jumper of mass $m$ can slide without friction along two parallel metal guides directed at an angle $\alpha$ to the horizontal and separated by a distance $b$ . The guides are connected at the bottom through an uncharged capacitor of capacitance $C$ , and the entire system is places in an upward magnetic field of induction $B$ . At the initial moment, the jumper is held at a distance $l$ from the foot of the hump. What will be it's velocity $v_f$ at the foot $?$

Answer comes in the form of $\Large v_{f}=\bigg ( \frac{\Phi l mg \sin \alpha }{\beta m+Cb^{\gamma}B^{\delta} \cos^{\phi} \alpha } \bigg )^{\lambda}$

Type your answer as $\Phi+\beta +\gamma +\delta +\phi +\lambda=?$

Details and Assumptions
1) The resistance of the guides and the jumper should be neglected.
2) $\Phi,\beta ,\gamma ,\delta ,\phi ,\lambda$ all are postive.

The problem is not original.

I will happy if anyone will upgrade this problem.