ElectroMechanics

A ring of radius 0.1 m is made out of a thin metallic wire of area of cross section 1 0 − 6 m 2 . The ring has a uniform charge of π coulombs .
Find the change in radius ( in mm ) of the ring when a charge of 1 0 − 8 coulomb is placed at the centre of the ring.
Details & Assumptions
-
Young's modulus of the metal 2 × 1 0 1 1 N / m 2
-
Answer in millimetres
Also try He is Invisible
The answer is 2.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The problem is incorrect. Actually, you also have to consider the field due to the ring itself, which doesn't converge. The potential energy of a uniform distribution on a ring is:
U = ∫ 0 2 π ∫ 0 2 π 2 ∣ ∣ ∣ ∣ sin ( 2 θ − ϕ ) ∣ ∣ ∣ ∣ k λ 2 R d θ d ϕ
which doesn't converge.
On expansion of ring the internal energy change will be divergent, and hence, the problem is incorrect
Krishna I had Added an Diagram for Your Question is it ok ?
Log in to reply
Thank you very much, nice solution by the way (Y).
Consider an circular arc element of charge on Ring , So when we place an 'Q' charge at the centre of ring Then due to Electrostatic Repulsion b/w charges an Extra Tension is created in Ring . which balance the repulsion b/w them .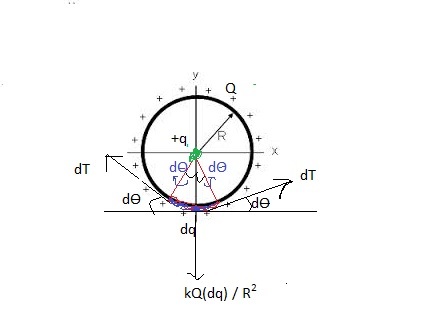
∴ R 2 K q ( d q ) = 2 d T sin ( d θ ) sin ( d θ ) ≈ d θ ∵ d q = 2 π R Q R ( 2 d θ ) d T = 2 π R 2 K Q q . . . ( 1 ) .
Now due to this extra Tension an Stress is developed in ring which further Cause the Expansion of radius (Due to Strain ) Now Using Hooks Law (By assuming that Young's modulus is so high so that Radius is Expand till Below it's Fracture point)
S t r e s s = Y × S t r a i n .
A d T = Y × ( R 2 π ( R + d R ) − 2 π R ) . . . ( 2 ) .
Using above equation we should get :
d R = 2 π R A Y K Q q .