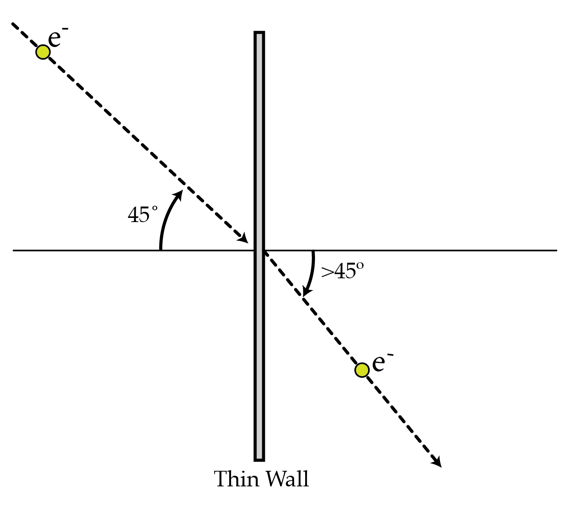
Electron's refraction

An electron passes through a thin wall. It assumed that energy is conserved for the electron. As a result, $-V_{1}e + K_{i} = -V_{2}e + K_{f}$ .

When you solve for $K_{f}$ , you get $K_{f} = 4 eV$ .

Since there is a potential difference between the two sides of the thin wall, there is an electric field inside of the thin wall. The electric field is in the horizontal direction, so it only has an effect on the x-component of the initial velocity. The y-component of the velocity remains constant.

As a result, $\sqrt{\frac{2K_{i}}{m}}\sin \alpha = \sqrt{\frac{2K_{f}}{m}}\sin \beta$

The $\sqrt{\frac{2}{m}}$ cancels out on both sides, so you can solve for $\beta$

$\beta = \arcsin (\sqrt{\frac{K_{i}}{K_{f}}} \sin \alpha)$

You get: $\boxed{\beta = 52.2}$

First we need to find the kinetic energy of the electron in the second region. E=K1+U1=5eV-3eV=2eV. Total energy is conserved. In region 2 on other side,again E=K2+U2. U2 is given to be -2eV. So K2=E-U2=4eV. Velocities are proportional to Sqrt(K). Next,observe since the plates are thin and parallel,we may treat it as a parallel plate capacitor. So the electric field acts normally to the plates. Since there is no force parallel to plates,the momentum taken parallel to plates is conserved. Therefore mv1sin45=mv2sin(beta). v1/v2=sqrt(K1/K2)=sqrt(5/4). We get sin(beta)=sqrt(5/8). Taking a calculator and finding inverse we get beta to be about 52 degrees.

Change in potential = -1.

=> Energy decreases by 1eV

=> Energy becomes 4 eV

=> Velocity becomes sqrt(4/5) times original velocity.

But the vertical component of velocity should remain same (intuition)

=> v sin(45) = v sqrt(4/5)*sin(B) => B= 52.2

You don't need any capacitor knowledge.