Electrostatic energy and combinatorics
A certain artificial molecule can be modelled as seven identical charges, arranged in a hexagon as shown in the figure. The chemical bonds are modelled as cords of length l. Based on dimensional analysis, the total energy of the system must be of the form
E
=
A
l
k
q
2
,
k
=
4
π
ϵ
0
1
where A is some numerical coefficient. Determine A.
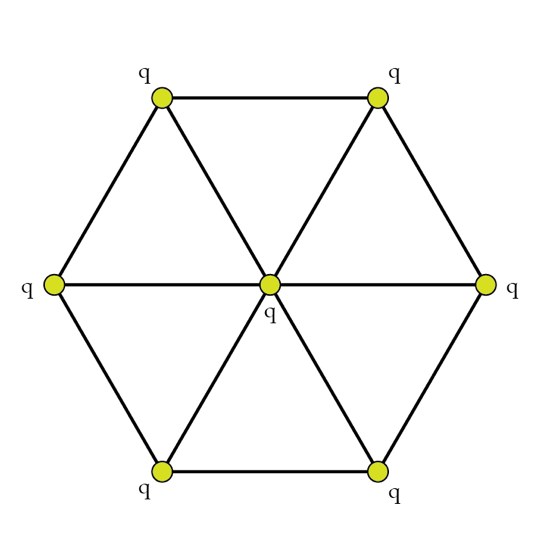
The answer is 16.96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
First of all, let's name the hexagon A B C D E F . We bring the central charge at a point. Next, bringing second charge q A requires some work to be done which is equal to l k . q 2 = U ( where I have assumed l k . q 2 = U ).
To bring second charge q B , we need to provide energy U + U .
Similarly, energy required for following charges :
q C = U + U + 3 U
q D = U + 2 U + 3 U + U
q E = U + U + 3 U + 2 U + 3 U
q F = U + U + 3 U + 2 U + 3 U + U
Summing all gives, total energy required = 1 2 U + 2 3 U + 1 . 5 U = 1 6 . 9 6 U
Hence, total energy required = 1 6 . 9 6 l k . q 2 .
From the potential energy we know that E=\frac {k q_1 q_2}{r} where r is a distance from both charges.There are seven identical charges based schematic figure so that combinatorics tell us that there are 21 potential energy on each of the two charges. By suming the potential energy from each of adjacent charges we obtain E=\frac{12 k q^2}{l}....(1) then by suming the potential energy from the charges that are separated by a distance 2 l apart we obtain E=\frac{3 k q^2}{2 l}...(2) Then we still have 6 other potential energy that are obtained from the charges that are separated by \sqrt{3} l.In the same way we obtain: E=\frac{2 \sqrt{3} k q^2}{l}....(3) Then the total energy of the system can be otained by suming equations (1),(2),and (3) ... Finally E=\frac{k q^2 16.964}{l}
adding potential energies due to each and every pair of charges we get A=12+(3/2)+(6/2^-{1/2})
There are 7 nodes. taking two at at time nC2=21.
Out of these 21 pairs,
distance of 3 pairs are of length 2L.
distance of 6 pairs are of length sqrt(3)L.
distance of 13 pairs are of length L.
Total energy of the system = 3kqq/(2L) + 6kqq/(sqrt(3)L) + 12kqq/L
=(kqq/L)*(3/2+6/sqrt(3)+12)
=(kqq/L)*(13.5+2sqrt(3))
comparing with A, we get A=13.5 +2sqrt(3) = 16.96
For anyone of the charge on the side of the hexagon, there is potential energy due to other charges at three different distance.
Due to adjacent charges and the charge at the center. Potential Energy U = 3 l k q 2
Due to charges right after the adjacent charges. Potential Energy U = 2 3 l k q 2
Due to charge opposite about the center Potential Energy U = 2 l k q 2
For charge at the center U = 6 l k q 2
There are in total 6 charges on the side, so the total potential energy due to charges on the side should be multiplied by 6. When adding them up, because each potential energy is counted twice, the total U should be divided by 2
U = 2 6 ( 3 l k q 2 + 2 3 l k q 2 + 2 l k q 2 ) + 6 l k q 2 = 1 6 . 9 6 l k q 2
A = 1 6 . 9 6