Electrostatic repulsion in a charged ring

The short answer: The Coulumb's Law states that the electric force is related to $\frac{Q^2}{r^2}$ , where $Q$ is the charge and $r$ is the distance between the two charges. In this case, since the circle remains the same size and dimension, $r$ can be treated as a constant. And since $Q^2$ is proportional to $f$ , when $f$ is increased by a factor of 10, $Q$ is increased by a factor of $\sqrt{10}$ , and the answer is thus $Q\sqrt{10}μC = 10\sqrt{10}μC$ or $31.6μC$

For those who think that the above isn't rigorous, the proof that $Q^2$ is proportional to force is as follows: Since the cross section of the ring is small, we can approximate the ring as a circle. By symmetry, the force pushing on any small segment of the ring will be pointing radially away from the ring.

We first consider the Electric field acting on any given point on the ring, which is given by $\int_0^{2\pi} \frac{k\sigma}{x^2}*\cos(\frac{pi-\theta}{2}) \mathrm{d}\theta$ where $\sigma = Q/ (2\pi r)$ is the charge density, $x$ is the distance between the point at $\theta = 0$ and another point. By cosine rule, $x^2 = 2r^2 - 2r^2 \cos \theta$ .

Substituting and integrating, we find that $E = \frac{kQ}{2r^2} * \frac{16}{3}$ . Since $F = EQ = \frac{8kQ^2}{3r^2}$ , the force is thus proportional to $Q^2$ .

Consider the electrostatic force between the halves of the ring. Right before the ring breaks we can write $T=\frac{1}{2} F$ where $T$ is the tension of the ring and $F$ is the interaction force between the semi-rings. 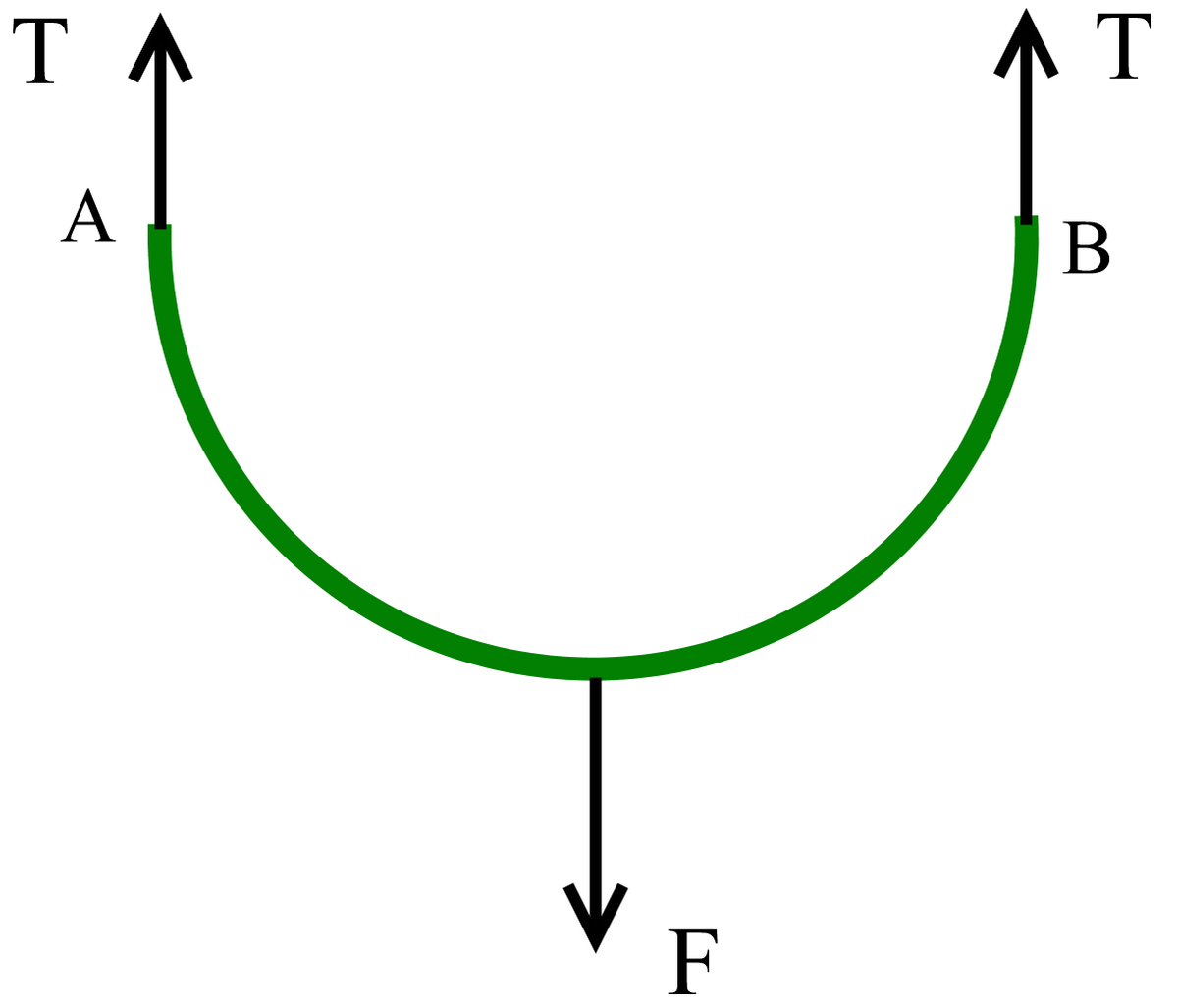The force $F$ could be, in principle, computed by integration. However, we do not to know the exact relation between $F$ , $Q$ and $R$ . It suffices to realize that it must be of the form: $F= \propto \frac{Q^{2}}{R^{2}}.$
Now, we can write $\frac{T_{2}}{T_{1}}=\frac{Q_{2}^2}{Q_{1}^{2}}$ which implies $Q_{2}=\sqrt{\frac{T_{2}}{T_{1}}} Q_{1}=\sqrt{10} Q_{1}=31.6 \mu\mbox{C}$ .

energy and hence the force acting for any system is proportional to square of the charge.when the ring becomes ten times resistant force required to break becomes ten times and hence minimum charge must increase by a factor of square root of ten which is 3.16 hence the result 31.6 μC.

We know that the repulsion that cause the ring to brake is dependent of the square of the charge on it. So we have that

F 2/F 1 = (Q 2/Q 1)^2 = 10

Q 2 = sqrt(10)Q 1 = 31.6E-6 Coulumb

The interesting thing is we dont have to derive tension formula,,,

it is fairly obvious as the tension arises from electrical interactions,, obviously it will be of the form

T= some constant times kq^2/r^2

this if the breaking tension becomes 10 T,, then q becomes root(10) times more,,, thus 31.6