Electrostatics corrected version

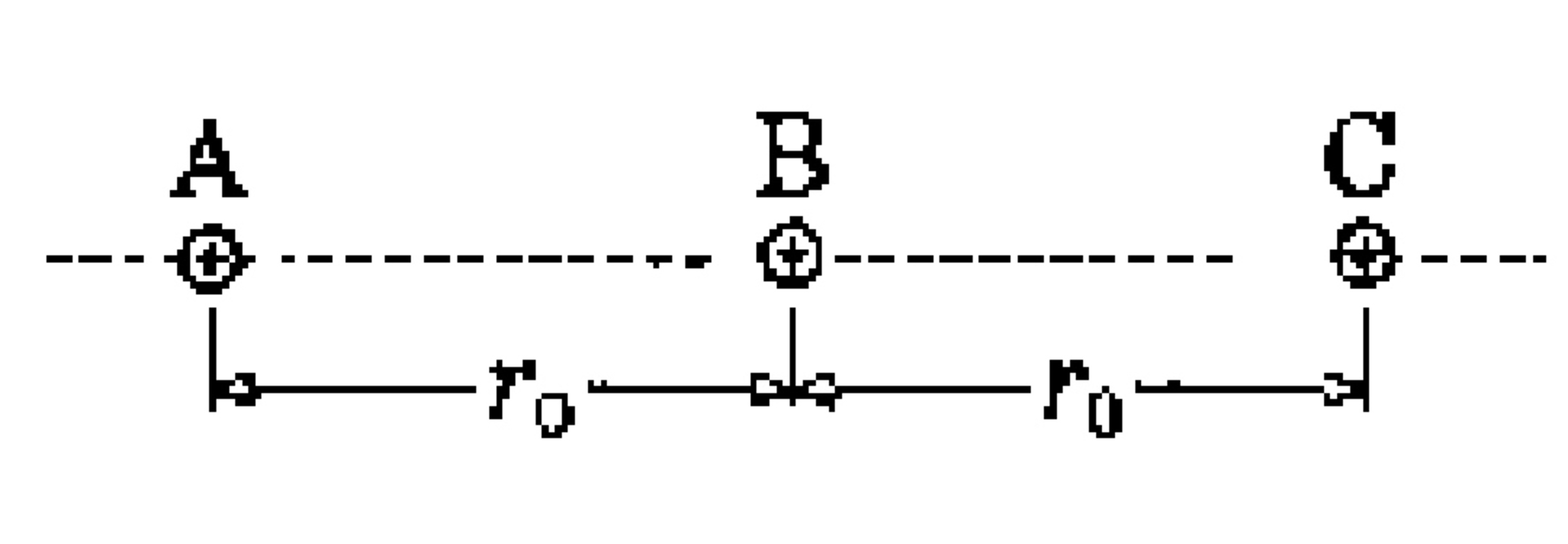
Electricity and Magnetism Level pending

Three particles A A , B B and C C of charges q q , q q and 2 q 2q and masses m m , 2 m 2m and 5 m 5m respectively are held in free space in a straight line at separation r 0 r_{0} .
between two adjacent particles as shown in the figure. All the three particles are released simultaneously. Find velocities of all the three particles when they reach so far from each other that electrostatic interactions between them can be neglected.
Type your answer as v A v B v C = ? v_{A}v_{B}v_{C}=?

Details and Assumptions
1) q = 1 q=1
2) ϵ 0 = 1 \epsilon_{0}=1
3) m = 1 m=1
4) r 0 = 1 r_{0}=1


The answer is 0.0237.

Talulah Riley by Talulah Riley , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Sep 13, 2020

Here's my numerical simulation. The end result is around 0.0238 0.0238 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
 
import math

# Basic constants

dt = 10.0**(-5.0)

q = 1.0
e0 = 1.0
m = 1.0
r0 = 1.0

########################################

# Mass-specific constants

k = 1.0/(4.0*math.pi*e0)

qA = q
qB = q
qC = 2.0*q

mA = m
mB = 2.0*m
mC = 5.0*m

########################################

# Initialize simulation

t = 0.0
count = 0

xA = -r0
xB = 0.0
xC = r0

xAd = 0.0
xBd = 0.0
xCd = 0.0

xAdd = 0.0
xBdd = 0.0
xCdd = 0.0

# Run simulation

while t <= 5000.0:

    xA = xA + xAd*dt
    xB = xB + xBd*dt
    xC = xC + xCd*dt

    xAd = xAd + xAdd*dt
    xBd = xBd + xBdd*dt
    xCd = xCd + xCdd*dt

    rAB = xA - xB
    rAC = xA - xC
    rBC = xB - xC

    FAB = k*qA*qB/(rAB**2.0)
    FAC = k*qA*qC/(rAC**2.0)
    FBC = k*qB*qC/(rBC**2.0)

    FA = -FAB - FAC
    FB = FAB - FBC
    FC = FAC + FBC

    xAdd = FA/mA
    xBdd = FB/mB
    xCdd = FC/mC

    t = t + dt
    count = count + 1

    if count % 100000 == 0:
        print t,(xAd*xBd*xCd),math.fabs(rAB),math.fabs(rBC)

########################################

# Result at t = 5000
4999.00001413 0.0237922472977 1990.32359722 1990.32359721

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase what are your views for solving this problem Anaylitically?

Talulah Riley - 9 months ago

Log in to reply

I haven't looked into it closely, but it seems like it would be difficult. A system of coupled differential equations

Steven Chase - 9 months ago

Maybe you could just use conservation of energy and momentum, and compare the t = 0 t = 0 and t = ∞ t = \infty cases

Steven Chase - 9 months ago

Log in to reply

@Steven Chase Yes that's what I am thinking.
But it will give 2 equations only. Right now we have 3 variables?
Somehow we need 1 more equation.

Talulah Riley - 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...