The flight to the center of the disc
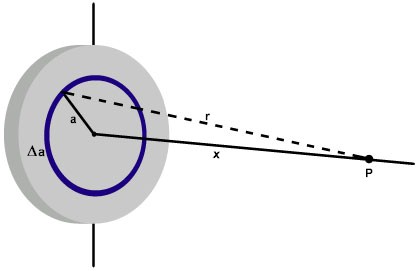A particle
P
having a charge of
−
1
μ
C
and mass 2 g is held at a distance of
x
=
1
m
from the center of a disc, as shown in the figure above. The disc has a radius of 2 m and surface charge density
6
.
8
4
×
1
0
−
4
C/m
2
.
The particle is released, and flies toward the disc. Find the velocity (in m/s ) of the particle when it has covered half the distance.
The answer is 112.141.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
Approximately 111.2 m/s.
The Electric field at a point on the axis of the disc at a distance x from the center can be calculated by simple calculus method (it is also usually used as a standard formula) which comes out to be
E = 2πkσ [1 - (x / √(x^2+R^2) )] N/C
where k is Coulomb’s constant, R is the radius and σ is the surface charge density of the disc.
Now, acceleration ‘a’ acting on the particle is :
a = Eq/m
where q and m is the charge and the mass of the particle respectively.
but a = v dv/dx where v is velocity.
Eq/m = v dv/dx
Now by substituting the values, integrating within the limits and solving, we get the velocity around 111.2 ± 2 m/s
Nice work. Another way to go is through potential energy. Similar to how you set up your E-field, we can say that potential goes as V ( z ) ∼ 0 ∫ R r 2 + z 2 r d r = z 2 + R 2 − z so that V = U / Q = 2 π k σ ( z 2 + R 2 − z )
Evaluating that at z = 1 & 1 / 2 , we find that Δ U ≈ 1 2 . 5 9 J and v ≈ 2 Δ U / m = 1 1 2 . 2 m/s .
Nice work. Another way to go is through potential energy. Similar to how you set up your E-field, we can say that potential goes as V ( z ) ∼ 0 ∫ R r 2 + z 2 r d r = z 2 + R 2 − z so that V = U / Q = 2 π k σ ( z 2 + R 2 − z )
Evaluating that at z = 1 & 1 / 2 , we find that Δ U ≈ 1 2 . 5 9 J and v ≈ 2 Δ U / m = 1 1 2 . 2 m/s .