Electrostats
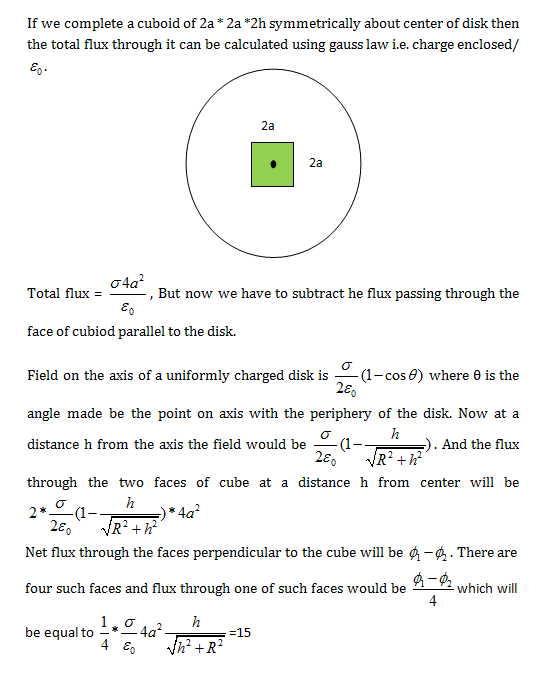
Consider a horizontal charged disk with center O and having surface charge density σ , and radius R , Consider a vertical rectangle of dimensions 2 a × 2 h , which cuts the disk at a distance a from its center, such that half of rectangle lies below the disk and half of it lies above the disk.Use a < < R to find the value of flux of electric field in N m 2 C − 1 through the rectangle to the nearest integer . The top view is shown below:

Details and assumptions
σ = 1 . 0 5 × 1 0 − 4 C m − 2
R = 3 m
a = 2 m m
h = 1 m
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice this is the most apparent solution.....If one wishes to avoid integration.
Use Gauss's law and a<<R use it to approximate that field on the axis at that height is uniform over the plane surface at that given height above and below the disk.
I guess you face problem of lack of knowledge of latex, please learn it as you can use it to make math elegant and to give complete solutions.Check for formatting guide . I am completing the solution below:
Here, we consider 3 more similar rectangles and cover them by horizontal lids to form a closed cuboid of dimensions 2 a × 2 a × 2 h , See the figure below, here, the square is the part of cuboid cutting the disk.
 Alternate text
Alternate text
Now , the flux of electric field through all such upright cylinders would be equal , (say ϕ 1 ), and through each one of horizontal lids ϕ 2 would be E ± h × ( 2 a ) 2 = ϵ 0 2 a 2 σ ( 1 − h 2 + R 2 h ) as (\ a << R)
By Gauss Law, total flux through the cuboid = ϵ 0 σ × 4 a 2 .
Hence, 4 ϕ 1 + 2 ϕ 2 = ϵ 0 σ × 4 a 2
⇒ ϕ 1 = ϵ 0 σ × a 2 h 2 + R 2 h
Log in to reply
Hey Jatin! You are in which class?
very excellent usage of Gauss' Law
Good question sir :)
do u call it a detailed solution........
jatin ...iam sorry..but i didnt understand..what have you done.....please help me out..i have problem in formula part
Log in to reply
Hi, I used nothing but the formula for electric field due to charged disk on its axis.