Elegance is the key - Part II
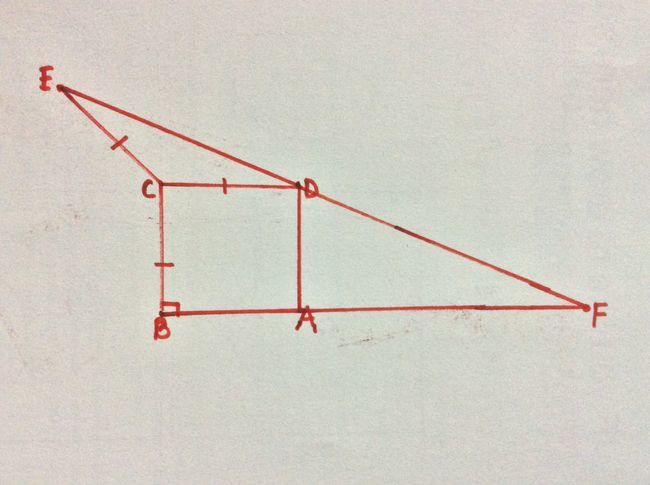 In the above figure, points
and
are collinear, and
. Also,
. The length of
is
, and the length of
is
. Then find the length of
in terms of
and
.
In the above figure, points
and
are collinear, and
. Also,
. The length of
is
, and the length of
is
. Then find the length of
in terms of
and
.
This is an original problem.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since E C = C D = C B , i.e. the points D , B and E are equidistant from point C , it implies that a circle can be drawn passing through through E , D and B with centre C .
Now, as E D F and B A F are straight lines and C B ⊥ B F , we clearly see that B F is a tangent, and E F is a secant to the circle C . Hence, from Tangent-Secant Theorem , we have F B 2 = F E ⋅ F D ⇒ F B = ( a + b ) b