Elegant 12
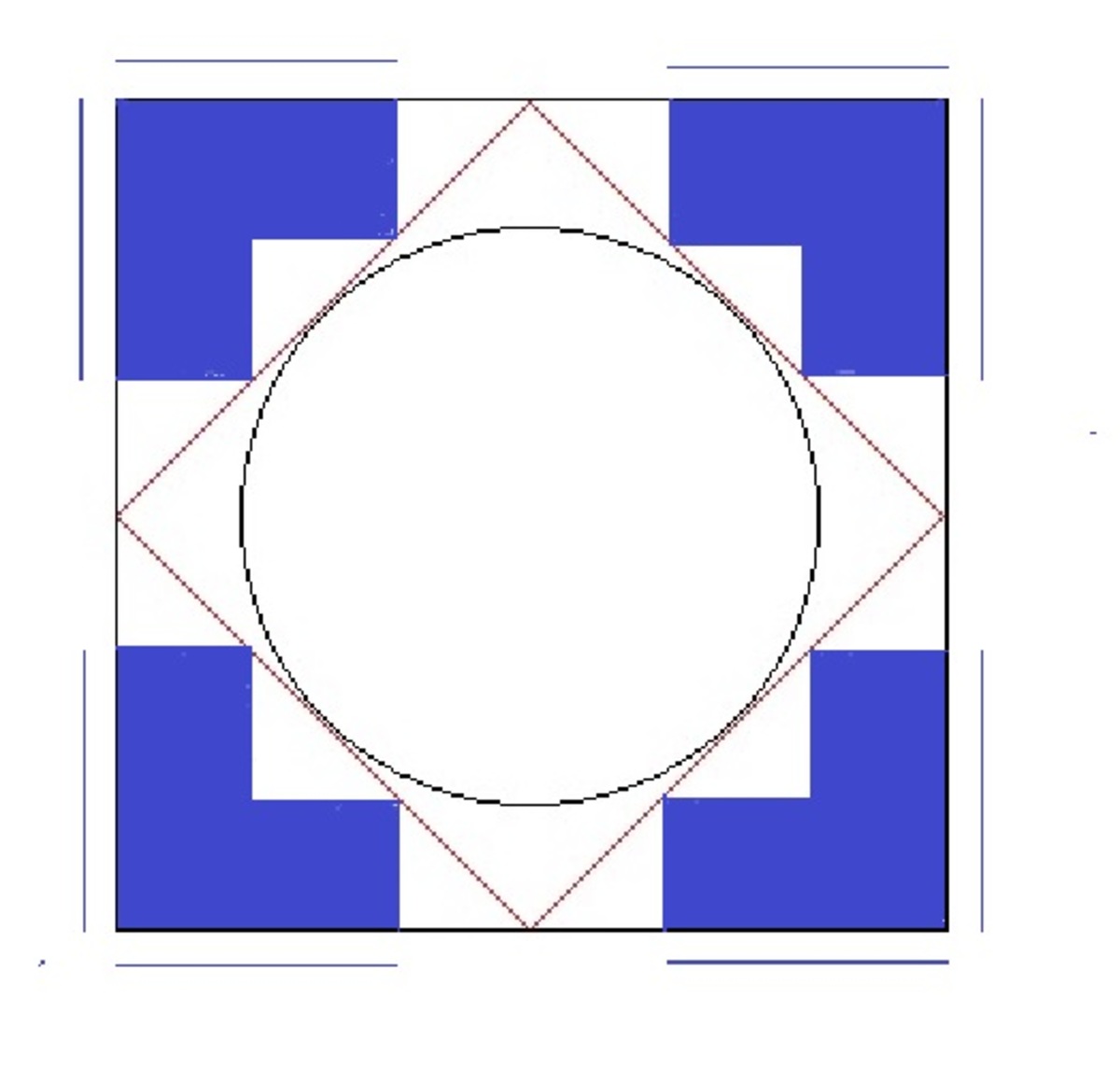
In traditional Buddhist architecture in Thailand, the square area surrounding the circular-based Chedi (Buddhist shrine) is characteristically modified to assimilate the structure's curvature with a method called "corner reduction 12": each square corner is cut so that 3 new right angles are formed, resulting in 12 angles in total as shown.
If we design the corner angles to touch the red tangents joining the square midpoints, and the smaller sides forming all the new right angles are equal, what is the fraction of the blue area compared to the big square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
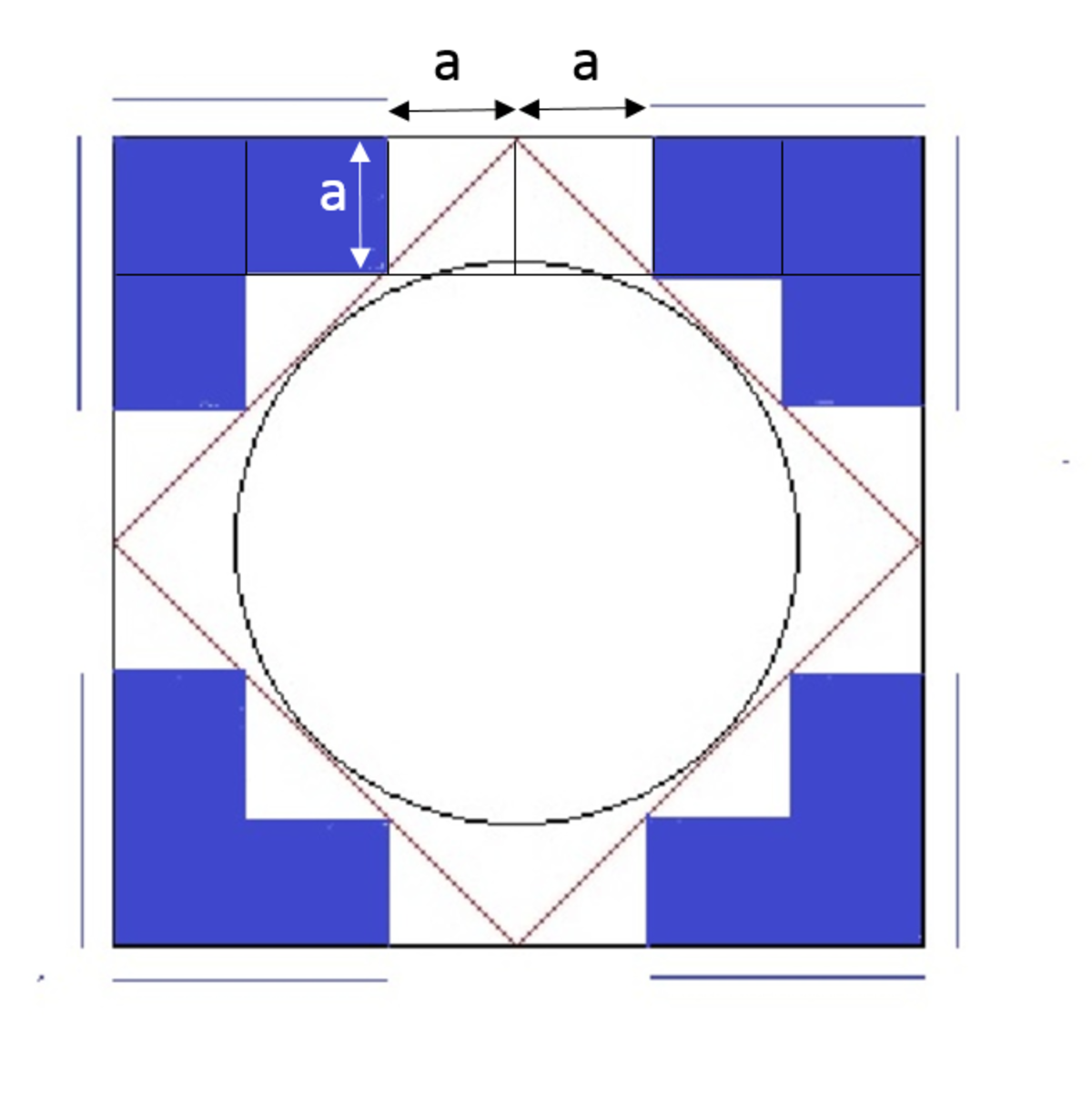
When we divide one of the four blue regions into smaller right triangles, we can see that all of these triangles are congruent as they are right-angled and have equal non-hypotenuse sides. Thus, 6 triangles will make up one blue corner region, and the total blue area will equal to 24 triangles.
Now considering the triangles touching the red tangents, we can see that at each corner, any of the three triangle is also congruent to the blue triangle. Therefore, the total area outside the tangents = (4\times (6+3)) = 36 triangles.
Then if draw perpendicular lines joining the square midpoints, we will see that red tangents act as the diagonals of the 4 congruent squares. Therefore, the area of the big square is halved by the red tangents, and the total area of the big square = 72 triangles.
Hence, the fraction of the blue area = 24/72 = 4/12 or 1/3.
Note: Each "reduced" corner area is 1/12 of the big square. It's an elegant 12 indeed!