How about rearranging these triangles?
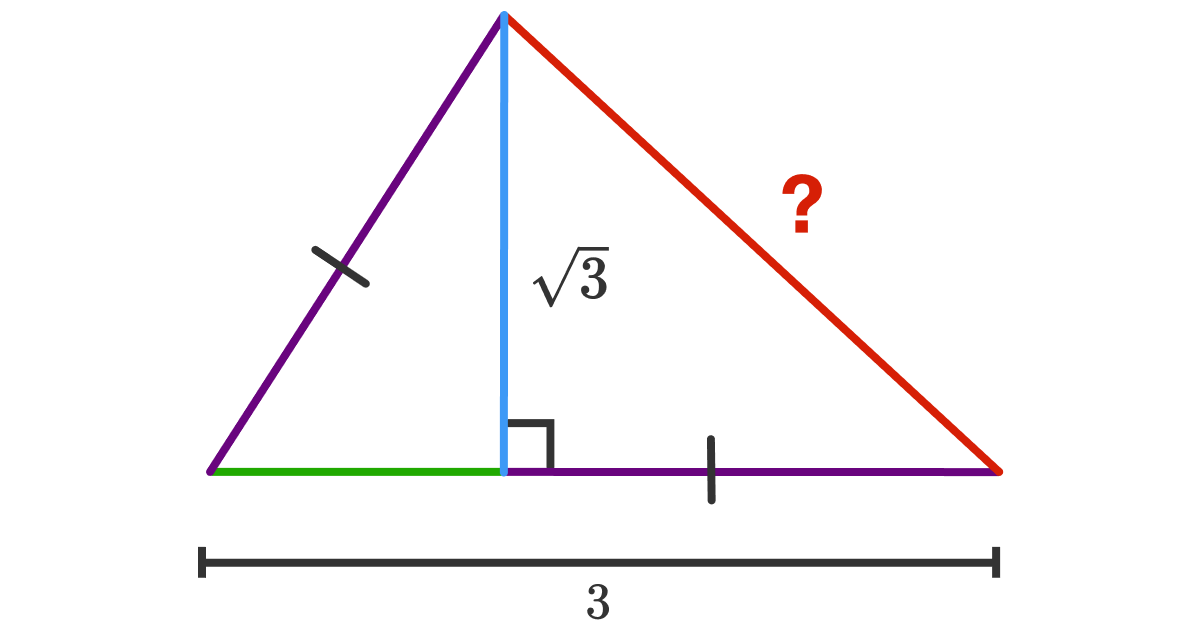
The above shows a triangle A B C with base A B = 3 and height C D = 3 . Point D lies on A B such that A D = B C . Find the length of A C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The crafty and elegant idea here is to create a rectangle. Let's call it B D C E . Since two diagonals in a rectangle are equal, B D = D E ! We thus have an isosceles triangle, and since the right-angled triangle B A E has a hypotenuse that is twice as long as its side, we realise that the two acute angles in the isosceles triangle are 3 0 ∘ each, which gives us another 3 0 − 6 0 − 9 0 triangle! And then we use Pythagoras' Theorem.
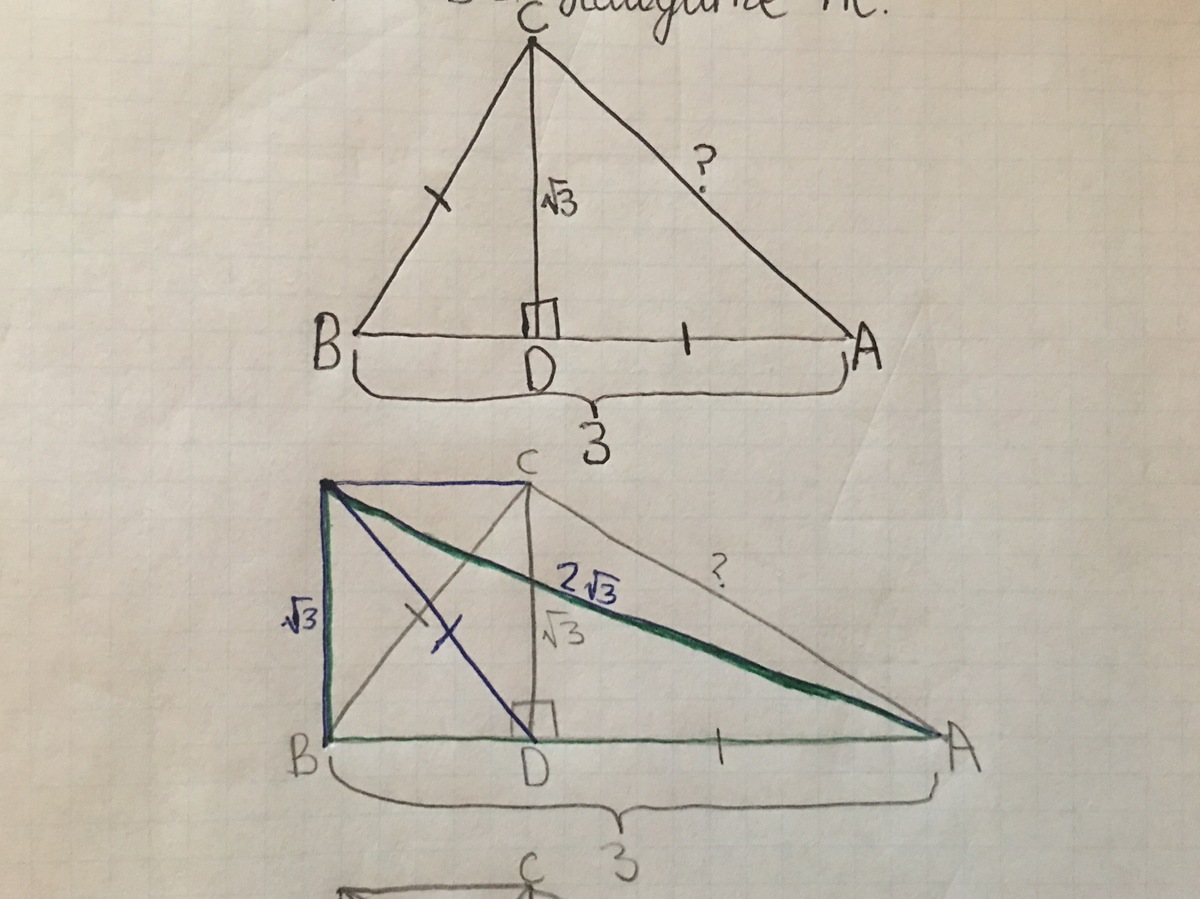
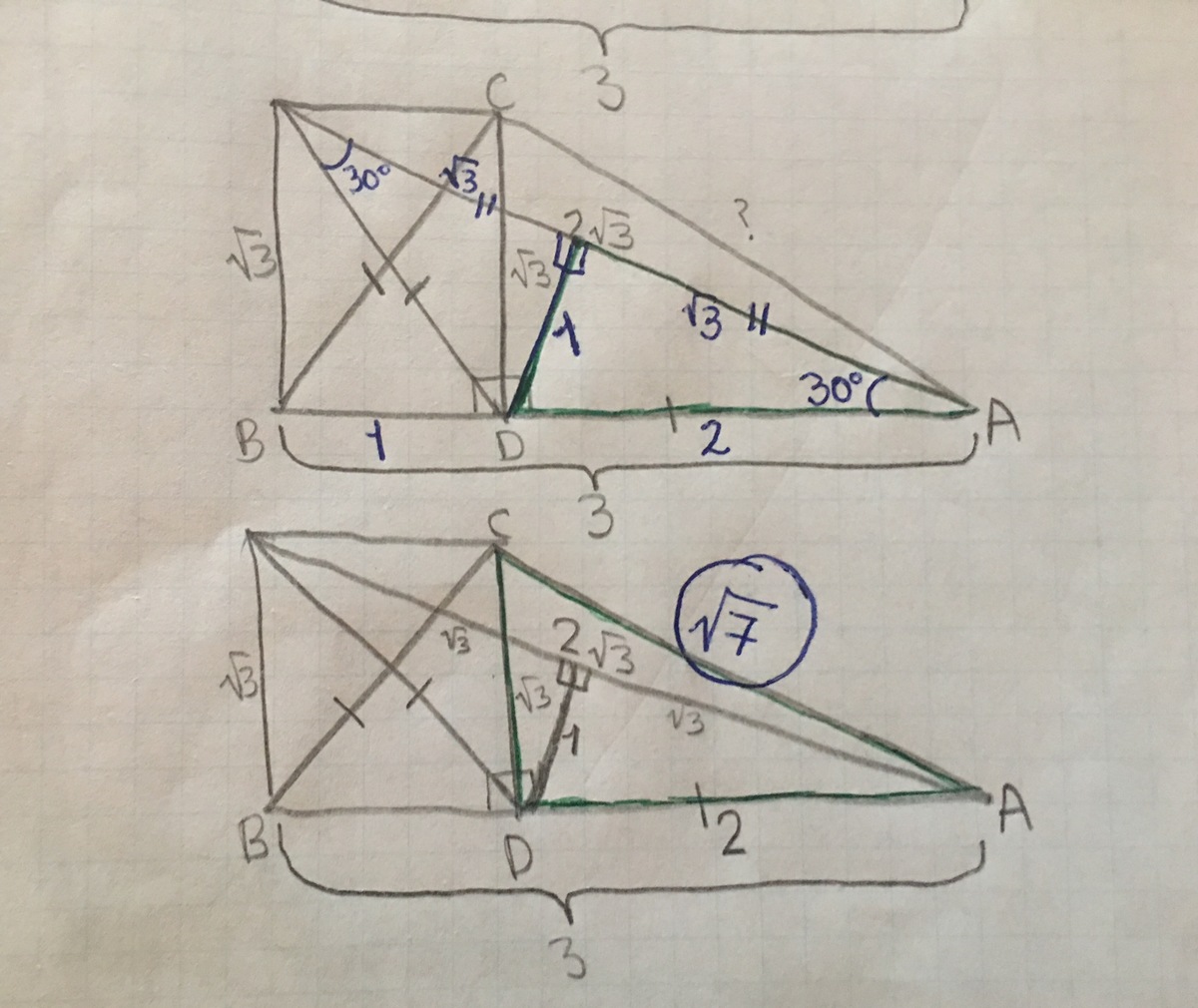
Alternatively, I suggest duplicating A D and putting it over B D to make a big isosceles triangle. That's another way, but my personal preference is to the former.
Or(orally) you could write A D = B C = x , then Pythagoras theorem in △ C B D will give: ( 3 − x ) 2 + 3 = x 2 ⟹ x = 2 . ∴ ? = 2 2 + 3 = 7 .
Log in to reply
That's what I did
Explanation is necessary for those people who are weak in mathematics .
Undoubtedly Praiseworthy work! But you make it so complex
Log in to reply
On the contrary, what I do here is much more elgant than mindless equation manipulation. This is geometry, and when something can be solved geometrically, the proof will necessarily be more beautiful.
You have my up vote for the explanation ! +1
The triangle Δ A D C is an right angled triangle.. So, from Pythagorean identity, A C 2 = C D 2 + A D 2 ⇒ A C 2 = 3 + A D 2 … … … … ( 1 ) Now the angle ∠ B A C in Δ A B C is an accute angle.. So, we can apply the expansion of Pythagorean theorem for accute angled triangle.. This is: B C 2 = A C 2 + A B 2 − 2 A B . A D ⇒ A D 2 = A C 2 + ( 3 ) 2 − 6 A D ;{Given, B C = A B } ⇒ A D 2 = 3 + A D 2 + 9 − 6 A D {From equation \color\green{(1)} } ⇒ A D = 2 … … ( 2 ) So, plugging A D = 2 in equation \color\green{(1)} , we get... A C = 3 + 2 2 \Rightarrow\boxed{\color\red{AC=\sqrt{7}}}
Let A D = B C = x , then applying Pythagorean theorem in △ C B D will give: ( 3 − x ) 2 + 3 = x 2 ⟹ x = 2 . ∴ ? = 2 2 + 3 = 7 .