Elephant VS Horse Powers
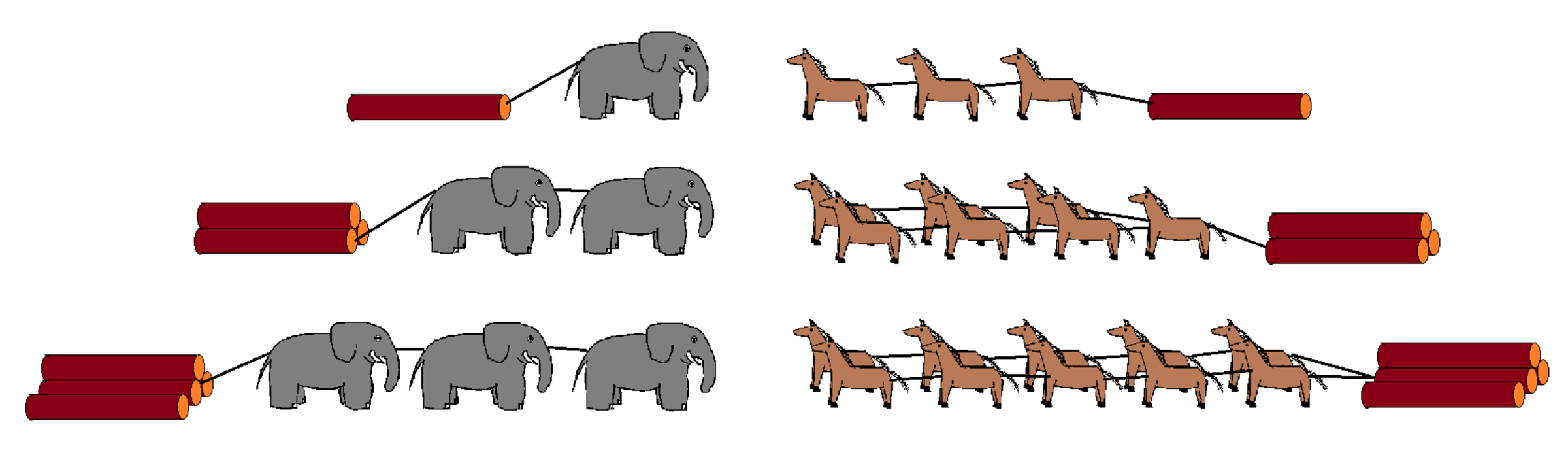
A young merchant of logging industry was deciding whether he should have bought elephants or horses for dragging the logs, and this was what he found from the farm owner:
For 1 log, only 1 elephant or at least 3 horses could complete the task.
For 3 logs, at least 2 elephants or at least 7 horses could complete the same task.
For 4 logs, at least 3 elephants or at least 10 horses could complete the same task.
Also, by asking the farm owner to test the animals, he also learnt that to drag 2 logs, he would need at least one elephant and one horse working together. After bargaining, he got the fair price of 25 gold coins for each elephant and 8 gold coins for each horse.
If he had 7 logs to be transported surely by these animals, what would be the least amount of gold coins he needed to invest? Assume each one of a kind has the same capacity and the animals could be tied together to combine their forces.
The answer is 116.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Linear programming algorithms
Let x be the amount of logs 1 elephant could drag and y be the amount for each horse.
For 1 log, x ≥ 1 because we know that one elephant could at least drag one log. On the other hand, 3 1 ≤ y ≤ 2 1 because we know that only 2 horses only couldn't complete the task and would need at least 3 horses.
Similarly, for 3 logs, we would obtain: 2 3 ≤ x ≤ 3 and 7 3 ≤ y ≤ 6 3
Finally, for 4 logs, we would obtain: 3 4 ≤ x ≤ 2 and 1 0 4 ≤ y ≤ 9 4
By combining all constraints, we can conclude that 2 3 ≤ x ≤ 2 and 7 3 ≤ y ≤ 9 4
From the last information, for 2 logs, x + y ≥ 2 . Then we can set up a linear programming for these inequalities as shown below:
The shaded area indicates the possible values of x and y , and so the minimal capacity lies within the four vertices of the polygon, specifically either on the point ( 7 1 1 , 7 3 ) or ( 9 1 4 , 9 4 ) .
Taking the ratios from those points we will get the ratio of y x as 7 1 1 × 3 7 = 3 1 1 ≈ 3 . 6 7 or 9 1 4 × 4 9 = 4 1 4 = 3 . 5 .
However, the ratio of the price is only 8 2 5 = 3 . 1 2 5 . Thus, it will be more cost-effective to buy elephants than the horses, and the strategy would be to buy as many elephants as possible and to compensate with some horses when some residual work load is left.
To ensure that, we have to think of the worst case scenario with least possible capacity of the elephants, which would be on point ( 9 1 4 , 9 4 ) .
For 7 logs, 7 × 1 4 9 = 2 9 = 4 . 5 . Then we would have two options: to buy 5 elephants or to buy 4 elephants plus 2 horses, which would suffice half of the elephant's capacity or about 2 3 . 5 = 1 . 7 5 horses. Clearly, the latter option is cheaper. Therefore, we need to invest at least 4 × 2 5 + 2 × 8 = 1 1 6 gold coins.
Checking on point ( 7 1 1 , 7 3 ) , 7 × 1 1 7 = 1 1 4 9 ≈ 4 . 4 5 . Again, 4 elephants should be bought and 1 1 5 × 3 1 1 = 3 5 ≈ 1 . 6 7 or 2 horses should be compensated to minimize the cost.