Eleven Square Theorem
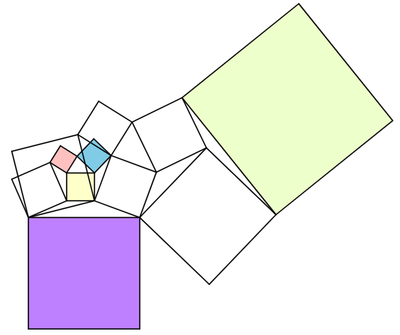
In the arrangement of 11 squares, the red, blue and yellow squares of respective areas of , and are pairwise tangent to each other.
Determine the area sum of the purple square and the green square.
The answer is 180.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If four squares are arranged as follows:
Then by the law of cosines on △ A B C , cos ∠ A C B = 2 a b a 2 + b 2 − c 2 .
And cos ∠ A ′ C B ′ = cos ( 1 8 0 ° − ∠ A C B ) = − cos A C B .
And by the law of cosines on △ A ′ B ′ C , c ′ 2 = a 2 + b 2 − 2 a b cos A ′ C B ′ = a 2 + b 2 + 2 a b cos A C B = a 2 + b 2 + 2 a b ⋅ 2 a b a 2 + b 2 − c 2 = 2 ( a 2 + b 2 ) − c 2 .
Using c ′ 2 = 2 ( a 2 + b 2 ) − c 2 on the red, blue, and yellow squares, the square to the immediate right has an area of 2 ( 3 + 4 ) − 2 = 1 2 , and the square to the immediate left has an area of 2 ( 2 + 4 ) − 3 = 9 . Then using it on the 2 , 4 , and 9 squares, the other square on the left has an area of 2 ( 4 + 9 ) − 2 = 2 4 .
Now label some points as follows:
From the area of the known squares, B ′ C = 3 , C A ′ = D A ′ = 2 , A ′ B ′ = A ′ F = 2 3 , E D = 3 , and E A ′ = 2 6 .
By the law of cosines on △ A ′ B ′ C , cos ∠ C A ′ B ′ = 2 ⋅ A ′ C ⋅ A ′ B ′ A ′ C 2 + A ′ B ′ 2 − C B ′ 2 = 2 ⋅ 2 ⋅ 2 3 4 + 1 2 − 3 = 2 4 1 3 3 .
By the law of cosines on △ A ′ D E , cos ∠ D A ′ E = 2 ⋅ A ′ D ⋅ A ′ E A ′ D 2 + A ′ E 2 − D E 2 = 2 ⋅ 2 ⋅ 2 6 4 + 2 4 − 9 = 4 8 1 9 6 .
Using sin θ = 1 − cos 2 θ , sin ∠ C A ′ B ′ = 1 − ( 2 4 1 3 3 ) 2 = 2 4 6 9 and sin ∠ D A ′ E = 1 − ( 4 8 1 9 6 ) 2 = 4 8 1 3 8 .
That means cos ∠ E A ′ F = cos ( 1 8 0 ° − ( ∠ C A ′ B ′ + ∠ D A ′ E ) ) = − cos ( ∠ C A ′ B ′ + ∠ D A ′ E ) = − cos ∠ C A ′ B ′ cos ∠ D A ′ E + sin ∠ C A ′ B ′ sin ∠ D A ′ E = − 2 4 1 3 3 ⋅ 4 8 1 9 6 + 2 4 6 9 ⋅ 4 8 1 3 8 = − 1 2 7 2 .
So by the law of cosines on △ A ′ E F , E F 2 = E A ′ 2 + A ′ F 2 − 2 ⋅ E A ′ ⋅ A ′ F ⋅ cos ∠ E A ′ F = 2 4 + 1 2 + 2 ⋅ 2 6 ⋅ 2 3 ⋅ 1 2 7 2 = 6 4 , which is also the area of the purple square.
Using c ′ 2 = 2 ( a 2 + b 2 ) − c 2 on the 1 2 , 2 4 , and 6 4 squares, the next square has an area of 2 ( 1 2 + 2 4 ) − 6 4 = 8 .
Using c ′ 2 = 2 ( a 2 + b 2 ) − c 2 on the 8 , 1 2 , and 2 4 squares, the next square has an area of 2 ( 8 + 1 2 ) − 2 4 = 1 6 .
Using c ′ 2 = 2 ( a 2 + b 2 ) − c 2 on the 8 , 1 2 , and 1 6 squares, the next square has an area of 2 ( 1 2 + 1 6 ) − 8 = 4 8 .
Using c ′ 2 = 2 ( a 2 + b 2 ) − c 2 on the 1 2 , 1 6 , and 4 8 squares, the next square has an area of 2 ( 1 6 + 4 8 ) − 1 2 = 1 1 6 .
Therefore, the area sum of the purple and green square is 6 4 + 1 1 6 = 1 8 0 .