Elixir Game

Probability Level 3

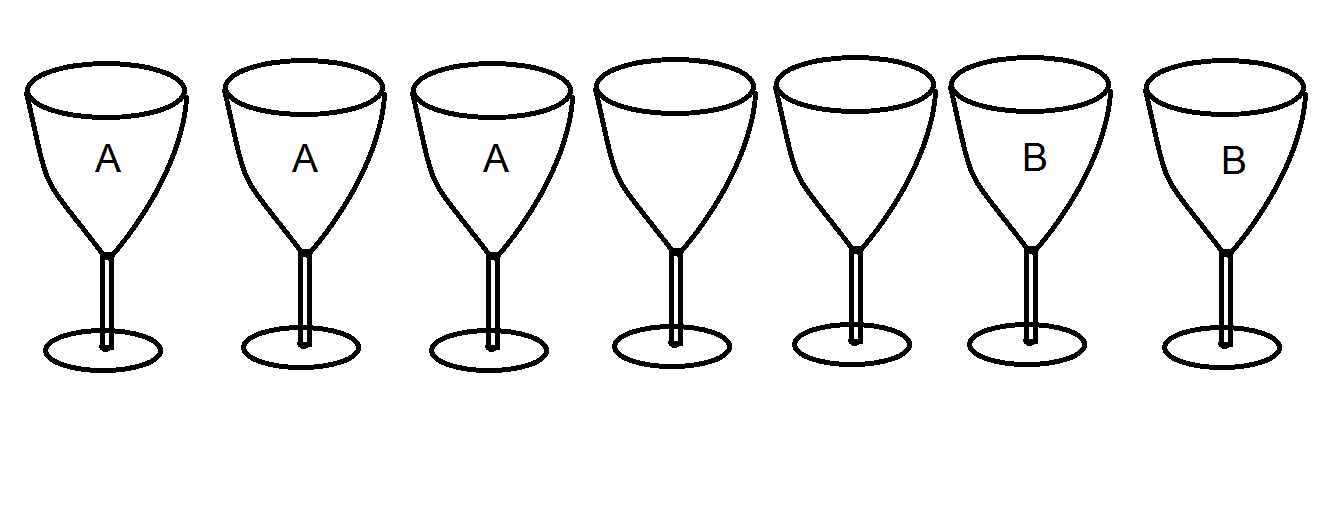
There are 7 cups all full of clear fluid, where 3 of them contain elixir $A$ , 2 contain elixir $B$ , and the remaining 2 pure water. All substances are colorless and tasteless, so you would have no way to distinguish any of them.

Elixir $A$ alone is poison even just for a cup. Once taken, you would need the same amount of elixir $B$ as an antidote, and you may take elixir $B$ before $A$ to protect the poison.

Nonetheless, drinking 2 cups of elixir $B$ without $A$ will be overdose and can also kill you as well. On the other hand, the water has no effects to either elixir.

If you have already drunk 3 cups of unknown combination, should you take the fourth cup to increase the survival rate?

Yes, you should Doesn't matter. The risk is the same Not enough information No, you shouldn't

1 solution

Worranat Pakornrat
Feb 7, 2017

To make the combination easier to visualize, let us denote elixir $A$ as $-1$ value, pure water as $0$ , and $B$ as $+1$ .

Now our desired outcome will be either $0$ or $1$ as negative result means excess of poison while $+2$ is also overdose.

For $3$ cups, the possible combinations are:

$-1+0+1$ : ${3}\choose{1}$ ${2}\choose{1}$ ${2}\choose{1}$ = $12$

$-1+1+1$ : ${3}\choose{1}$ ${2}\choose{2}$ = $3$

$0+0+1$ : ${2}\choose{2}$ ${2}\choose{1}$ = $2$

Thus, there are $17$ ways to survive this game of $3$ cups. The whole combination is ${7}\choose{3}$ = $35$

For $4$ cups, the possible combinations are:

$-1-1+1+1$ : ${3}\choose{2}$ ${2}\choose{2}$ = $3$

$-1+0+1+1$ : ${3}\choose{1}$ ${2}\choose{1}$ ${2}\choose{2}$ = $6$

$-1+0+0+1$ : ${3}\choose{1}$ ${2}\choose{2}$ ${2}\choose{1}$ = $6$

Thus, there are $15$ ways to survive this game of $4$ cups. The whole combination is ${7}\choose{4}$ = $35$

With same denominator, the probability to survive this game is slightly higher with $3$ cups trial. As a result, the fourth cup shouldn't be drunk.

Nice problem. I guess the last set of calculations should be "For 4 cups" rather than 3, (and "Thus, there are 15 ways to survive this game of 4 cups.").

When you state that 2 cups of antidote can kill you, this is only if you have had these 2 cups in the absence of any cups of poison in the 3 or 4 cups you have chosen. I first thought that, if drinking in sequence, if your first 2 glasses were antidote you would just instantly drop dead, but from your calculations you are looking at the result of the 3 or 4 cups taken as a whole and not worrying about the sequence in which they were consumed. The final answer of "No, you shouldn't" is the same with my interpretation, in any event.

Brian Charlesworth - 4 years, 4 months ago

Thank you. It's already edited.

Yes, your interpretation is correct. This is the art of medicine. Any substance can be poison if you take too much of it. So better to consult your doctor. :)

Worranat Pakornrat - 4 years, 4 months ago

The phrasing could be greatly improved. Currently, the phrasing seems to imply that

"Elixir A alone is poisonous. Once taken, you would need... " -> You cannot drink B before A to preemptively neutralize the poison.
"Nonetheless, drinking 2 cups of elixir B can also kill you as well" -> If you have drunk 2 cups of B, regardless of how many cups of A you drunk, you are still dead.

Calvin Lin Staff - 4 years, 4 months ago

Hi, I've edited the phrasing. So actually, the order is flexible: you may take $B$ before $A$ to neutralize the poison, and taking only $2 B$ will result in overdose.

This is how the real medicine works. Any substance can be poison, and some certain poison can be antidote as well. For example, alcohol is antidote for ethyleneglycol, but drinking too much alcohol can be poisoning as well.

Welcome to the world of medicine. :)

Worranat Pakornrat - 4 years, 4 months ago

Elixir Game

1 solution

0 pending reports